Particle A is suspended by a string tied at point O from the roof of a room. The same particle is also tied to one of the walls of that room, at point B. Find the tension in OA before and after AB is cut.
To solve the problem of finding the tension in the string OA before and after the string AB is cut, we can follow these steps:
Step 1: Understand the Setup
We have a particle A suspended by two strings: one string (OA) is attached to the roof at point O, and the other string (AB) is attached to the wall at point B. The particle is in equilibrium before the string AB is cut.
Step 2: Draw the Free Body Diagram
Draw a diagram showing the forces acting on particle A. The forces include:
- The tension T1 in the string OA acting at an angle θ from the vertical.
- The tension T2 in the string AB acting horizontally.
- The weight of the particle, which is mg acting downward.
Step 3: Apply Equilibrium Conditions
Since the particle is in equilibrium before the string AB is cut, the net forces in both horizontal and vertical directions must be zero.
Horizontal Forces:
- The horizontal component of T1 (T1 sin θ) must balance T2.
T1sinθ−T2=0(1)
Vertical Forces:
- The vertical component of T1 (T1 cos θ) must balance the weight of the particle (mg).
T1cosθ−mg=0(2)
Step 4: Solve for T1
From equation (2), we can express T1 in terms of mg and θ:
T1cosθ=mg
T1=mgcosθ
This is the tension in the string OA before the string AB is cut.
Step 5: Analyze the Situation After Cutting the String AB
When the string AB is cut, the particle A will start to fall freely under the influence of gravity. At the moment the string AB is cut, the tension T1 in string OA will change.
Step 6: Determine the New Tension T1 After Cutting
After cutting the string AB, the only forces acting on the particle A are its weight (mg) and the tension T1 in the string OA. At this moment, the particle will start moving in a circular path about point O.
- The net force acting on the particle in the radial direction is the tension T1, which must provide the centripetal force required for circular motion. However, since the particle is at the point of release, the speed is zero, and thus the centripetal force is also zero.
In this case, the tension T1 is equal to the component of the weight acting in the radial direction:
T1=mgcosθ
Step 7: Summary of Tensions
- Before cutting the string AB:
T1=mgcosθ
- After cutting the string AB:
T1=mgcosθ
We have a particle A suspended by two strings: one string (OA) is attached to the roof at point O, and the other string (AB) is attached to the wall at point B. The particle is in equilibrium before the string AB is cut.
Draw a diagram showing the forces acting on particle A. The forces include:
- The tension T1 in the string OA acting at an angle θ from the vertical.
- The tension T2 in the string AB acting horizontally.
- The weight of the particle, which is mg acting downward.
Since the particle is in equilibrium before the string AB is cut, the net forces in both horizontal and vertical directions must be zero.
- The horizontal component of T1 (T1 sin θ) must balance T2.
T1sinθ−T2=0(1)
- The vertical component of T1 (T1 cos θ) must balance the weight of the particle (mg).
T1cosθ−mg=0(2)
From equation (2), we can express T1 in terms of mg and θ:
T1=mgcosθ
When the string AB is cut, the particle A will start to fall freely under the influence of gravity. At the moment the string AB is cut, the tension T1 in string OA will change.
After cutting the string AB, the only forces acting on the particle A are its weight (mg) and the tension T1 in the string OA. At this moment, the particle will start moving in a circular path about point O.
- Before cutting the string AB:
T1=mgcosθ
- After cutting the string AB:
T1=mgcosθ
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PROBLEMS
56 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(SINGLE CORRECT CHOICE TYPE)
40 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
A unifrom rod of mass m and length L is kept on a horizontal table with L4 length on the table. The end B is tied to a string as shown in the figure. The string attached to the end B is cut and the rod starts rotating about point C. Find the normal reaction from the table on the earth as soon as the string is cut.

View Solution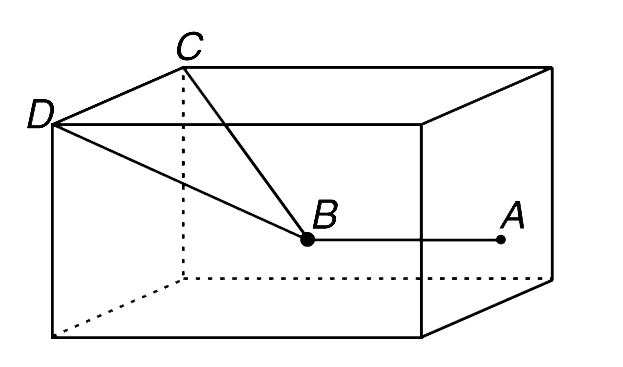
A room is in shape of a cube . A heavy ball (B) is suspended at the centre of the room tied to three inextensible strings as shown. String BA is horizontal with A being the centre point of the wall. Find the ratio of tension in the string BA and BC.
View Solution
Knowledge Check
IF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
Acentripetal forceBthe difference between centripetal force and weight of the stoneCthe addition of the centripetal force and weight of the stoneDweight of the stoneA particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
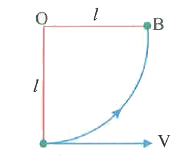 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2glA particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
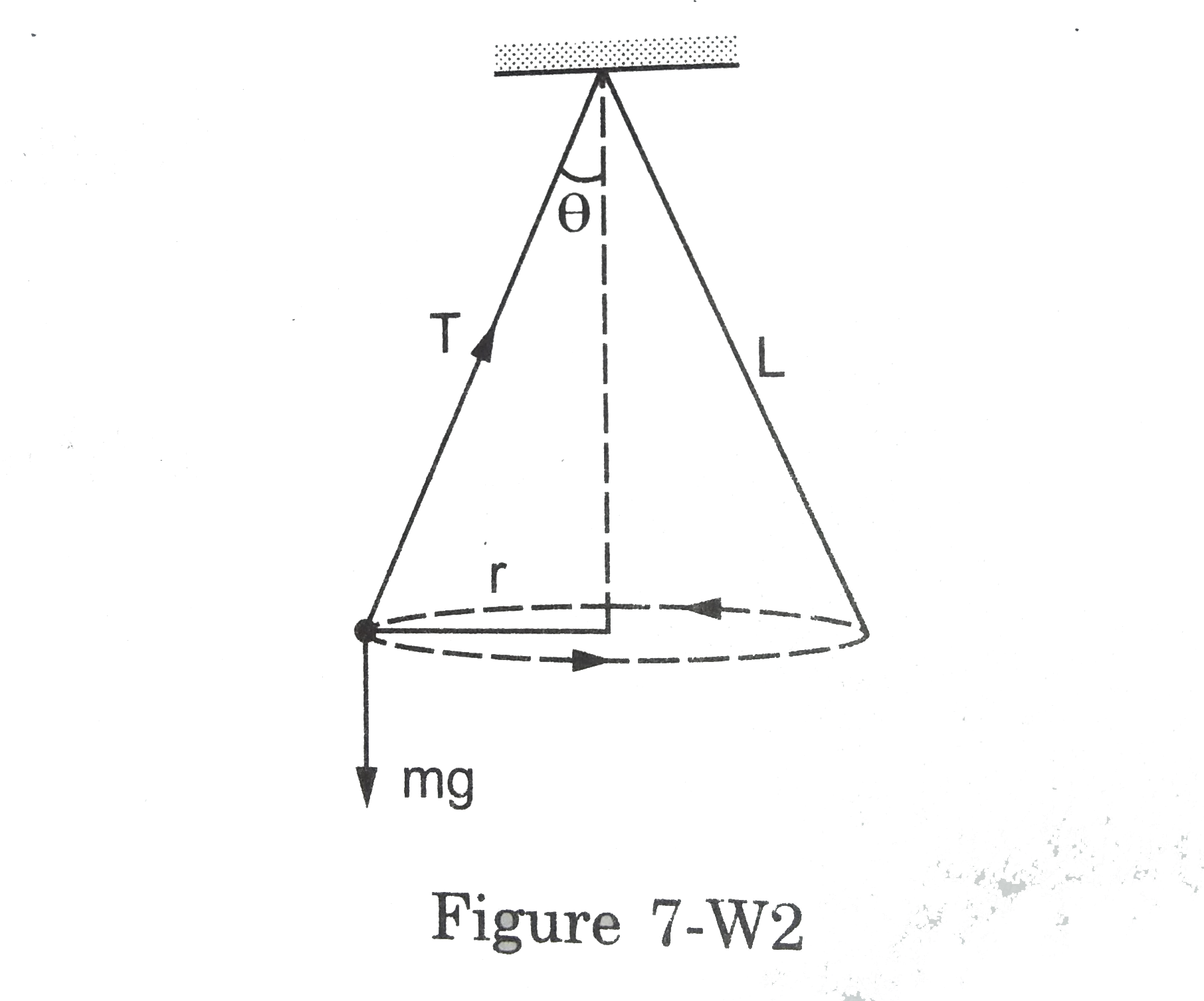
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14
A pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
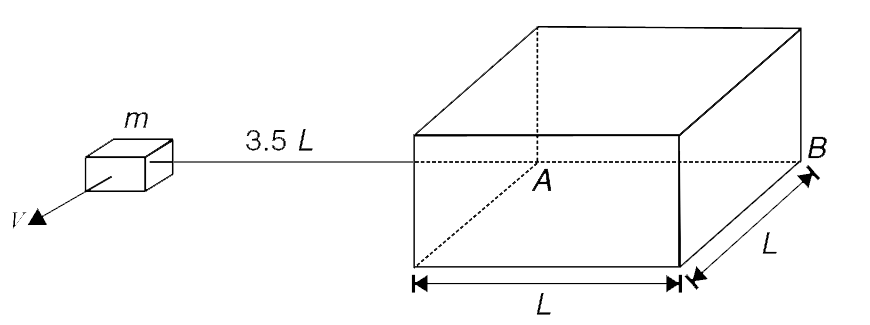
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View SolutionA particle of mass m=2 kg is suspended in a vertical plane by two strings - one horizontal and the other inclined to the vertical by α=30∘. Find the tension of the inclined string (a) an instant before the horizontal one is cut, (b) an instant after the horizontal one is cut.
View SolutionA particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View Solution
