The world's largest ball of string is about 2 m in radius. To the nearest order of magnitude, what is the total length L of the string in the ball?
To find the total length L of the string in the ball with a radius of 2 meters, we can follow these steps:
Step 1: Calculate the Volume of the Sphere
The formula for the volume V of a sphere is given by:
V=43πr3
Where r is the radius of the sphere. In this case, the radius r=2 meters.
Step 2: Substitute the Radius into the Volume Formula
Substituting r=2 meters into the volume formula:
V=43π(2)3
Calculating (2)3:
(2)3=8
So,
V=43π⋅8=323π cubic meters
Step 3: Approximate the Value of π
For simplicity, we can approximate π as 3.14:
V≈323⋅3.14
Calculating this gives:
V≈32⋅3.143≈100.483≈33.49 cubic meters
Step 4: Relate Volume to Length of String
Assuming the string can be modeled as a very thin cuboid, we can express the volume V in terms of the length L of the string and its cross-sectional area A:
V=L⋅A
If we assume the cross-sectional area A is very small, we can denote it as d2 where d is the diameter of the string. For simplicity, we can assume d is on the order of 0.01 m (1 cm), thus:
A≈(0.01)2=0.0001 square meters
Step 5: Solve for Length L
Now we can rearrange the equation to solve for L:
L=VA=33.490.0001=334900 meters
Step 6: Convert to Order of Magnitude
To express this in terms of order of magnitude, we can write:
L≈3.35×105 meters
To the nearest order of magnitude, this is:
L≈106 meters
Step 7: Convert to Kilometers
Since 1 kilometer=1000 meters:
L≈1000 kilometers
Final Answer
Thus, the total length L of the string in the ball is approximately 106 meters or 1000 kilometers.
---
The formula for the volume V of a sphere is given by:
Substituting r=2 meters into the volume formula:
For simplicity, we can approximate π as 3.14:
Assuming the string can be modeled as a very thin cuboid, we can express the volume V in terms of the length L of the string and its cross-sectional area A:
Now we can rearrange the equation to solve for L:
To express this in terms of order of magnitude, we can write:
Since 1 kilometer=1000 meters:
Thus, the total length L of the string in the ball is approximately 106 meters or 1000 kilometers.
Topper's Solved these Questions
- UNITS AND MEASUREMENT Book:RESNICK AND HALLIDAYChapter:UNITS AND MEASUREMENT Exercise:PROBLEM
Explore 20 Videos
- UNITS AND MEASUREMENT Book:RESNICK AND HALLIDAYChapter:UNITS AND MEASUREMENT Exercise:PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
Explore 31 Videos
- THE NUCLEUSBook:RESNICK AND HALLIDAYChapter:THE NUCLEUSExercise:PRACTICE QUESTIONS(Integer Type)
Explore 7 Videos
- VECTORS Book:RESNICK AND HALLIDAYChapter:VECTORS Exercise:PRACTICE QUESTIONS
Explore 39 Videos
Similar Questions
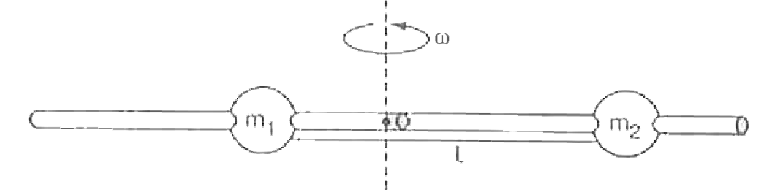
Two balls of masses m1=0.5kgandm2=0.3kg are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with ω=110 rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if l=20 cm is the length of the string. Is the equilibrium of the balls stable ?
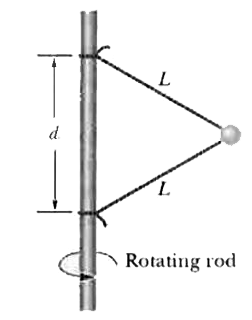
View SolutionIn fig 1.34 kg ball is connected by means of two mass less strings, each of length L=1.70m, to a vertical, rotating rod. The strings are tied to the rod with separation d=1.70 m and are taut. The tenion in the upper string is 35N. What are the (a) tension in the lower string, (b) magnitude of the net (b) magnitude of the net force →Fnet on the all, and (c) speed of the ball? (d) What is the direction of →Fnet?
View Solution
Knowledge Check
A stretched string of length L fixed at both the ends has nodes, where n>2. What is the length of the string in terms of n and λ ?
AL=nλ2BL=nλCL=(n+1)λ2DL=(n−1)λ2On the centre of a frictionless table, a small hole is made, through which a weightless string of lenth 2l is inserted. On the two ends of the strings, two balls of the same mass m are attached, Arrangement is made in such a way that half of the string is on the table top and half is hanging below. The ball on the table top is made to move in a circular path with a constant speed v, What is the centripetal acceleration of the moving ball?
AmvlBgCzeroD2mvlThe linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
AmLBmLCmL2DmL3
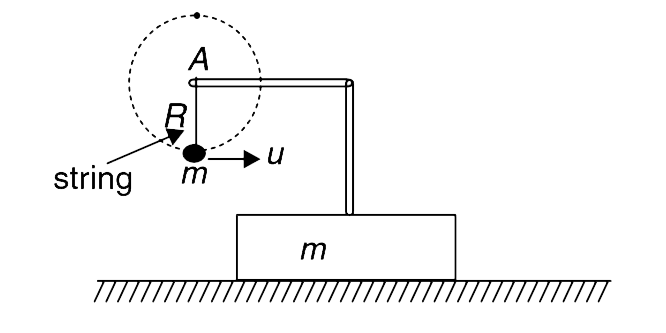
A small ball of mass m is suspended from the end A of a L shaped mass less rigid frame which is fixed to a block of mass m. The block is placed on a smooth table. The ball is given a horizontal impulse so as to impart it a velocity of u. The ball beings to rotate in a circle of radius R about the point A, while the block and the frame slide on the table. Find the tension in the string, to which the ball is attached, at the instant the ball is at the top most position. The rod does not interfere with the string during the motion.
View SolutionTwo identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
View SolutionA ball of mass m with a charge q can rotate in a vertical plane at the end of a string of length l in a uniform electrostatic field whose lines of force are directed upwards. What horizontal velocity must be imparted to the ball in the upper position so that the tension in the string in the lower position of the ball is 1.5 times than the weight of the ball?
View SolutionWhen a string is divided into three segments of length l1,l2 and l3 the fundamental frequencies of these three segments are f1,f2 and f3 respectively. The original fundamental frequency f of the string is
View SolutionThe linear mass density 'μ' of the string is (where, mass of the string = m, length of the string = L)
View Solution

