A disc is rotating with angular velocity ω. A force F acts at a point whose position vector with respect to the axis of rotation is r. The power associated with torque due to the force is given by
(→r×→F).→ω
(→r×→F)×→ω
→r×(→F.→ω)
→r.(→F×→ω)
The correct Answer is:A
Step by step video, text & image solution for A disc is rotating with angular velocity omega. A force F acts at a point whose position vector with respect to the axis of rotation is r. The power associated with torque due to the force is given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (GRAVITATION)
Explore 25 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (COLLISION AND CENTRE OF MASS )
Explore 12 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
A disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionTwo discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
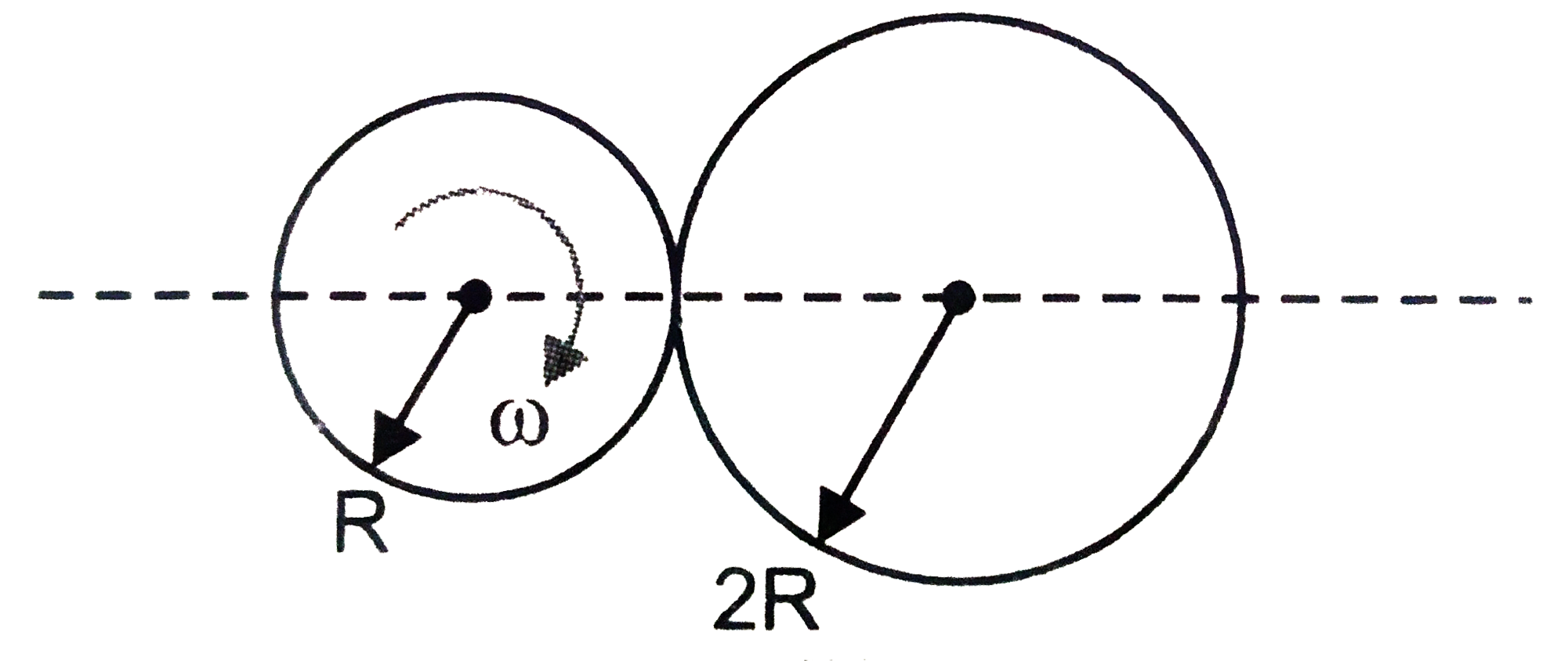
View Solution
Knowledge Check
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
ALinear momentumBAngular momentumCkinetic energyDMoment of inertiaA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
AIωBL=EωCL=2EωDL=ωE
Let a force F be acting on a body free to rotate about a point O and let r be the position vector of any point P on the line of action of the force. Then torque (τ) of this force about point O is defined as τ=r×F Given, F=(2ˆi+3ˆj−ˆk)Nandr=(ˆi−ˆj+6ˆk)m. Find the torque of this force.
View SolutionA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
View SolutionFind the torque about the origin when a force of 3ˆj N acts on a particle whose position vector is 2ˆk m
View SolutionA force →F=4ˆi−10ˆj acts on a body at a point having position vector −5ˆi−3ˆj relative to origin of co-ordinates on the axis of rotation. The torque acting on the body is
View SolutionDuring rotation of a body, the position vector is along X-axis and force vector is along Y-axis, The direction of torque vector is
View Solution

