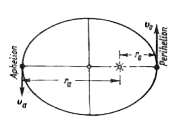
Let the speed of the planet at the perihelion $P$ in figure be $v_{P}$ and the Sun planet distance $S P$ be $r_{P}$ . Relater $r_{P}, v_{P}$ to the corresponding quantities at the aphelion $(r_{A}, v_{A})$ . Will the planet take equal times to transverse $B A C$ and $C P B$ ?

Video Solution

Text Solution

Verified by Experts

$∵$ angular momentum $L = m_{P} r_{P} v_{P} = m_{P} r_{A} v_{A}$
$∴ \frac{v_{P}}{v_{A}} = \frac{r_{A}}{r_{P}}$ since $r_{A} > r_{P}, v_{P} > v_{A}$ .
The area SBAC bounded by the ellipse and the radius vectors SB and SC is larger than SBPC in Fig. From Kepler's second law, equal areas are swept in equal time intervals. Hence the planet will take a longer time to traverse BAC than CPB.

Updated on:21/07/2023

A: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .
AIf both Assertion & Reason are true . And the reason is the correct explanation of the assertion , then mark (1)
BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion , then mark (2)
CIf Assertion is true statement but Reason is false , then mark (3)
DIt will move the same speed , tangentially to the spacecraft
If r denotes the mean distance of a planet from the sun and T is the time period of planet, then
A $r \propto T^{2 / 3}$
B $r \propto T^{3 / 2}$
C $r \propto T^{1 / 3}$
D $r \propto T$
The period of revolution of a planet around the sun is 8 times that of the earth. If the mean distance of that planet from the sun is r, then mean distance of earth from the sun is
A $r / 2$
B $2 r$
C $r / 4$
D $4 r$