A large cylindrical rod of length L is made by joining two identical rods of copper and steel of length (L2) each. The rods are completely insulated from the surroundings. If the free end of copper rod is maintained at 100∘C and that of steel at 0∘C then the temperature of junction is (Thermal conductivity of copper is 9 times that of steel)
90∘C
50∘C
10∘C
67∘C
The correct Answer is:A
To solve the problem, we need to find the temperature of the junction (T) between the copper and steel rods. We will use the concept of thermal conductivity and the principle of heat transfer through the rods.
1. Identify the given values:
- Length of each rod = L2
- Temperature at the free end of the copper rod = 100∘C
- Temperature at the free end of the steel rod = 0∘C
- Let the thermal conductivity of steel be K. Therefore, the thermal conductivity of copper is 9K.
2. Calculate the thermal resistance of each rod:
- The thermal resistance R of a rod can be calculated using the formula:
R=LkA
- For the steel rod:
Rsteel=L2KA=L2KA
- For the copper rod:
Rcopper=L29KA=L18KA
3. Set up the equation for heat transfer:
- Since the rods are in series, the heat flow through both rods is the same. Thus, we can write:
T−0Rsteel=100−TRcopper
- Substituting the thermal resistances:
TL2KA=100−TL18KA
4. Simplify the equation:
- Cross-multiplying gives:
T⋅L18KA=(100−T)⋅L2KA
- Cancel LKA from both sides:
T18=100−T2
5. Solve for T:
- Cross-multiplying again:
2T=18(100−T)
2T=1800−18T
20T=1800
T=180020=90∘C
6. Conclusion:
- The temperature of the junction is T=90∘C.
- Length of each rod = L2
- Temperature at the free end of the copper rod = 100∘C
- Temperature at the free end of the steel rod = 0∘C
- Let the thermal conductivity of steel be K. Therefore, the thermal conductivity of copper is 9K.
- The thermal resistance R of a rod can be calculated using the formula:
R=LkA
- For the steel rod:
Rsteel=L2KA=L2KA
- For the copper rod:
Rcopper=L29KA=L18KA
- Since the rods are in series, the heat flow through both rods is the same. Thus, we can write:
T−0Rsteel=100−TRcopper
- Substituting the thermal resistances:
TL2KA=100−TL18KA
- Cross-multiplying gives:
T⋅L18KA=(100−T)⋅L2KA
- Cancel LKA from both sides:
T18=100−T2
- Cross-multiplying again:
2T=18(100−T)
2T=1800−18T
20T=1800
T=180020=90∘C
- The temperature of the junction is T=90∘C.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTER Book:DISHA PUBLICATIONChapter:THERMAL PROPERTIES OF MATTER Exercise:Exercise-1: Concept Builder (Topicwise)
Explore 69 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION Book:DISHA PUBLICATIONChapter:SYSTEM OF PARTICLES & ROTATIONAL MOTION Exercise:EXERCISE-2 : CONCEPT APPLICATOR
Explore 28 Videos
- THERMODYNAMICS Book:DISHA PUBLICATIONChapter:THERMODYNAMICS Exercise:EXERCISE -2 : CONCEPT APPLICATOR
Explore 29 Videos
Similar Questions
Figure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1^(@)C^(-1)andtˆofsteel=46Wm^(-1)(∘)C−1 .

View SolutionThe thermal conductivity of copper is four times that of brass. Two rods of copper and brass of same length and cross-section are joined end to end. The free end of copper rod is at 0∘C and that of brass rod at 100∘C. Calculate the temperature of junction at equilibrium. neglect radiation losses.
View Solution
Knowledge Check
Figure shows a copper rod joined to a steel rod. The rods have equal length and equal cross-sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C. Find the temperature θ at the junction of the rods. Conductivity of copper
=390W/m−∘C and that of steel =46W/m−∘C.
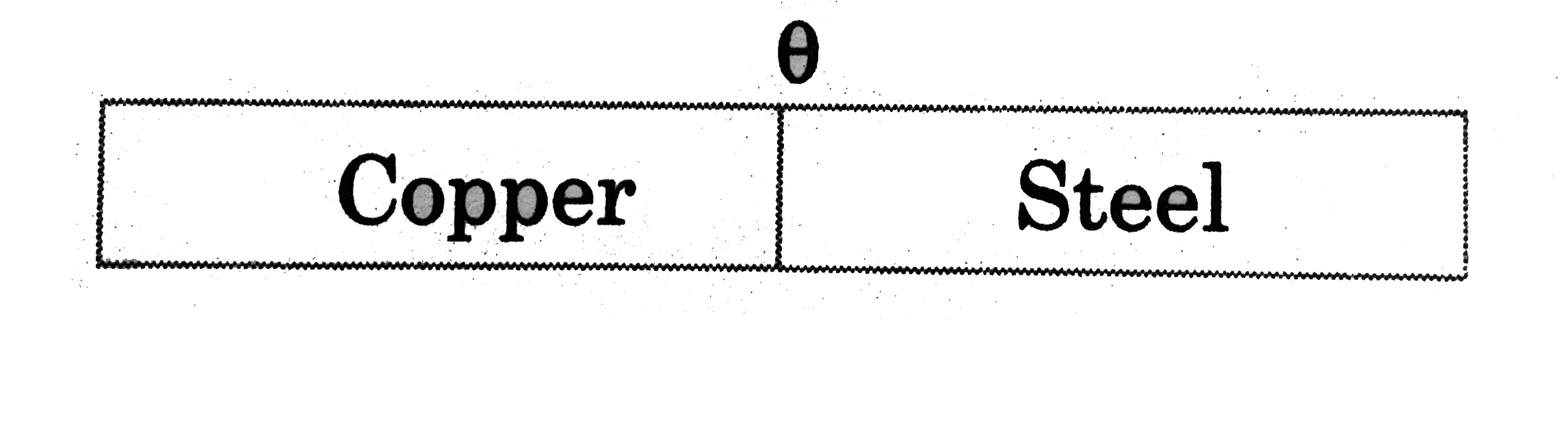 .A20.55∘CB30.55∘CC10.55∘CDNone of these
.A20.55∘CB30.55∘CC10.55∘CDNone of theseCylinder copper rod of length 1m and a cylinder steel rod of length 1.5m are joined together end to end. The cross sectional area of eac rod is 3.14cm. The free ends of steel rod and copper rods are maintained at 0∘C and 100∘C respectively. The surfaces of rods are thermally insulated. Find the temperature of copper steel junction. (Given thermal conductivity of steel =46J/m−s.∘C and the thermal conductivity of copper =386J/m−s.∘C)
A40∘B60∘C93∘D80.64∘CTwo rods of copper and brass having the same length and cross - section are joined end to end. The free end of the copper is at 0∘C and of brass is at 80∘C in steady-state. If thermal conductivity of copper is 4 times of that of brass find the temp. at junction of two rods
A80∘CB64∘CC20∘CD16∘C
+2.0 -0.0 An engineer joined a rod in which 50 cm is copper and 100 cm is steel from end to end together. Both have the circular cross-section with diameter 3 cm. If the free end of copper and steel are maintained at the temperature 100°C and 0°C respectively. Determine the temperature of the copper-steel junction. (Assume the thermal conductivity of copper and steel are 386 J/m - 5-°C. 46 J/m - 5-°C respectively) 50 cm 100 cm 100°C Copper Steel 0°C
View Solution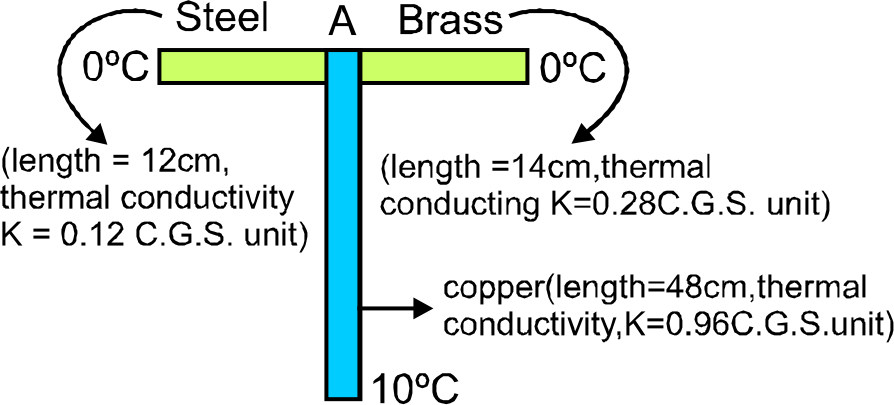
Three rods of copper, brass and steel are joined together to form T shape as shown in figure. The cross sectional area of each rod is 4cm2 the end of copper rod is maintained at 10∘C and the ends of brass and steel rods at 0∘C assume there is no loss of heat to surrounding. What is temperature of junction point A in .∘C
View SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
View SolutionTwo rods having thermal conductivity in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined by face to face. If the temperature of the free end of the first rod is 100∘C and free end of the second rod is 20∘C . Then temperature of the junction is
View Solution

