Oil is filled in a cylindrical container up to height 4m. A small hole of area 'p' is punched in the wall of the container at a height 1.52m from the bottom. The cross sectional area of the container is Q. Ifpq=0.1 then v is (where vis the velocity of oil coming out of the hole)
5√2
6√3
8√2
7√5
The correct Answer is:A
To solve the problem, we will use Bernoulli's equation and the principle of conservation of mass. Here’s a step-by-step solution:
Step 1: Identify the heights involved
- The height of the oil column is h1=4m.
- The height of the hole from the bottom is h2=1.52m.
- The difference in height h=h1−h2=4−1.52=2.48m.
Step 2: Apply Bernoulli's equation
According to Bernoulli's theorem, for two points in a fluid flow, we have:
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
Since the hole is open to the atmosphere, the pressure at both points can be considered equal (let's denote it as P). Therefore, we can simplify the equation:
ρgh1+12ρv21=ρgh2+12ρv22
Step 3: Assume initial conditions
Assuming the velocity of the oil in the container at the surface is negligible (i.e., v1≈0), we can simplify further:
ρgh1=ρgh2+12ρv22
Step 4: Cancel out the density
Since the density ρ is common on both sides, we can cancel it out:
gh1=gh2+12v22
Step 5: Rearranging the equation
Rearranging gives us:
g(h1−h2)=12v22
Step 6: Substitute the values
Substituting the values we have:
g=9.8m/s2
h1−h2=2.48m
Thus,
9.8×2.48=12v22
Step 7: Solve for v2
Calculating the left side:
24.304=12v22
Multiplying both sides by 2:
48.608=v22
Taking the square root:
v2=√48.608≈6.96m/s
Step 8: Relate v to V
From the problem, we know that:
pQ=0.1⟹v=10V
Thus, the velocity v of the oil coming out of the hole is:
v≈6.96m/s
Final Answer:
The velocity of oil coming out of the hole is approximately 6.96m/s.
---
- The height of the oil column is h1=4m.
- The height of the hole from the bottom is h2=1.52m.
- The difference in height h=h1−h2=4−1.52=2.48m.
According to Bernoulli's theorem, for two points in a fluid flow, we have:
Assuming the velocity of the oil in the container at the surface is negligible (i.e., v1≈0), we can simplify further:
Since the density ρ is common on both sides, we can cancel it out:
Rearranging gives us:
Substituting the values we have:
h1−h2=2.48m
Calculating the left side:
From the problem, we know that:
The velocity of oil coming out of the hole is approximately 6.96m/s.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS Book:DISHA PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDS Exercise:EXERCISE-2 CONCEPT APPLICATOR
Explore 24 Videos
- MECHANICAL PROPERTIES OF FLUIDS Book:DISHA PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDS Exercise:EXERCISE-2 CONCEPT APPLICATOR
Explore 24 Videos
- MAGNETISM AND MATTERBook:DISHA PUBLICATIONChapter:MAGNETISM AND MATTERExercise:EXERCISE-2:CONCEPT APPLICATOR
Explore 31 Videos
- MOTION IN A PLANE Book:DISHA PUBLICATIONChapter:MOTION IN A PLANE Exercise:Exercise -2 : CONCEPT APPLICATOR
Explore 28 Videos
Similar Questions
A fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionWater is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
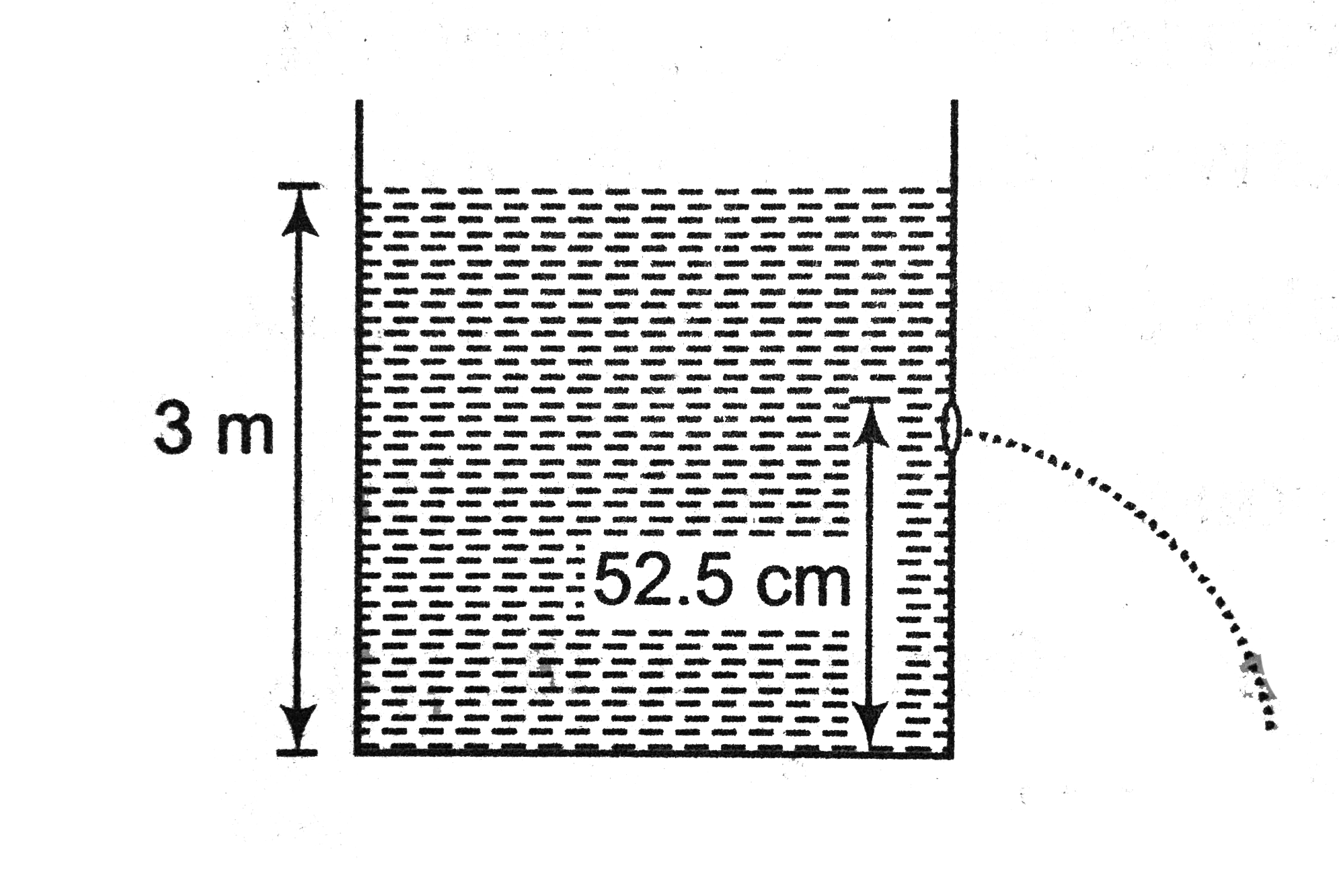
View Solution
Knowledge Check
Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
A(a) 50B(b) 51C(c) 48D(d) 51.5A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
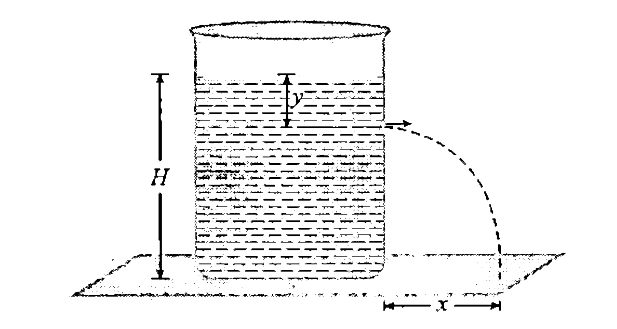 A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−h
A2√h(H−h)B√h(H−h)C2√h2H−hD√h2H−hA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2
What is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
View SolutionA cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionA cylindrical tank is filled with water to a level of 4 m. A hole is opened at a height of 60 cm from bottom. The ratio of the area of the hole to that at cross-sectinal area at cylinder is 0.2. Then the velocity with which water is coming out is (g=10m/s2)
View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t=0 till water comes out of hole, pick the correct statement:
View Solution

