Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
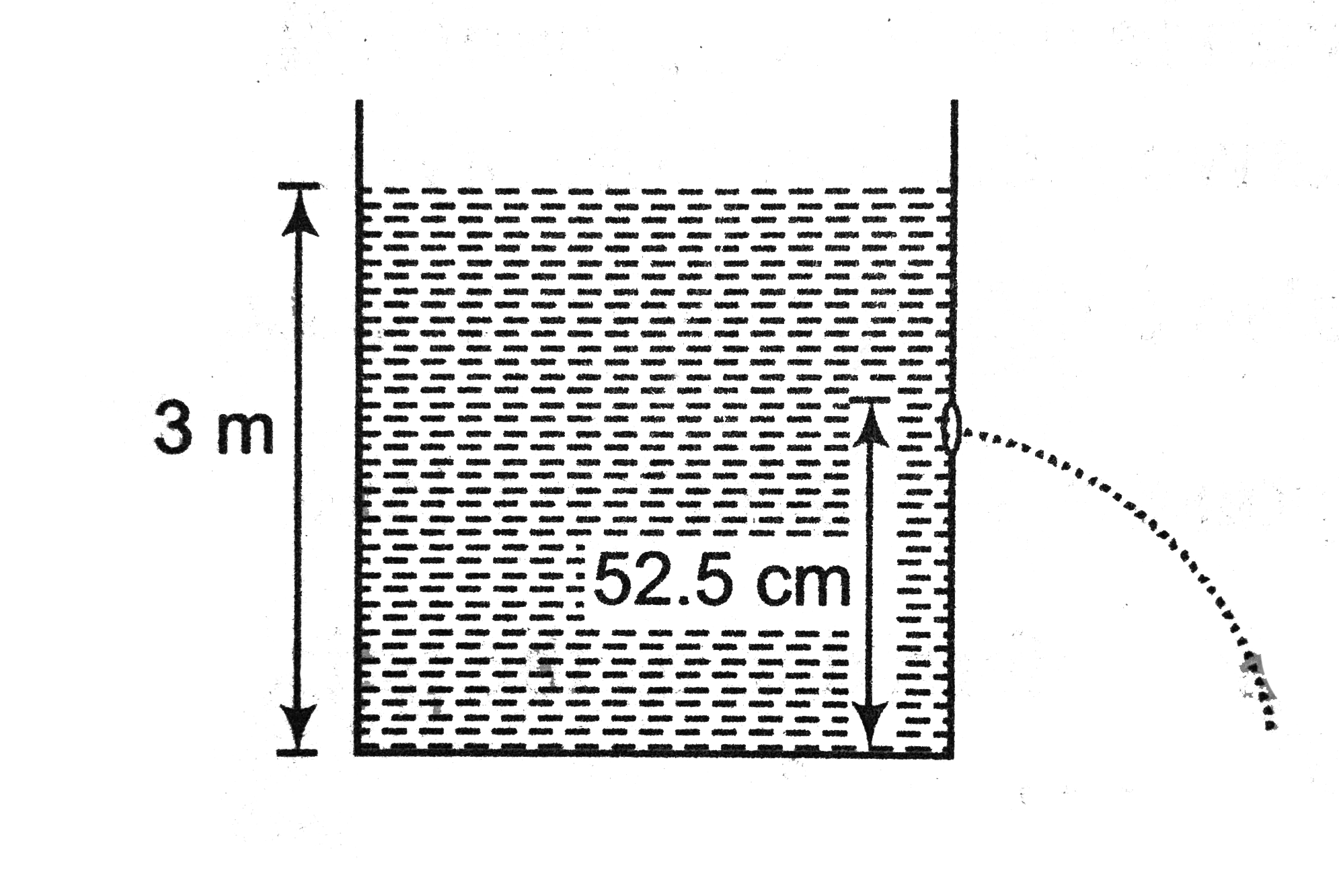
50m2/s2
50.5m2/s2
51m2/s2
52m2/s2
The correct Answer is:A
Applying continuity equation at 1 and 2, we have
A1v1=A2v2...(i)
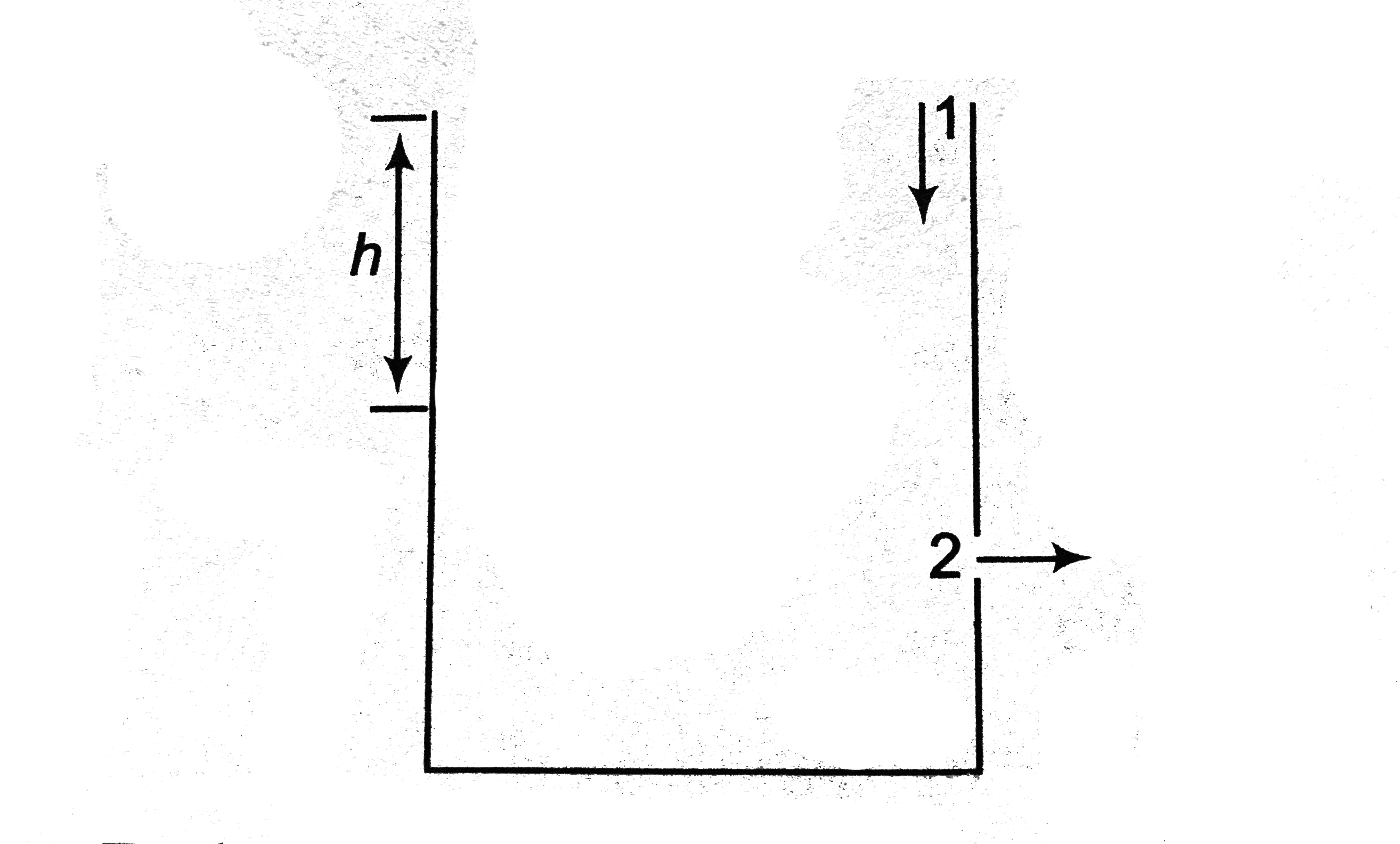
Further applying Bernoulli's equation at these two points, we have
p0+ρgh+12ρv21=p0+0+12ρv22...(ii)
Solving Eqs. (i) and (ii), we have v22=2ghI−A22A21
Substituting the values, we have
v22=2×10×2.4751−(0.1)2=50m2/s2.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.6
4 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.7
4 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.4
4 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
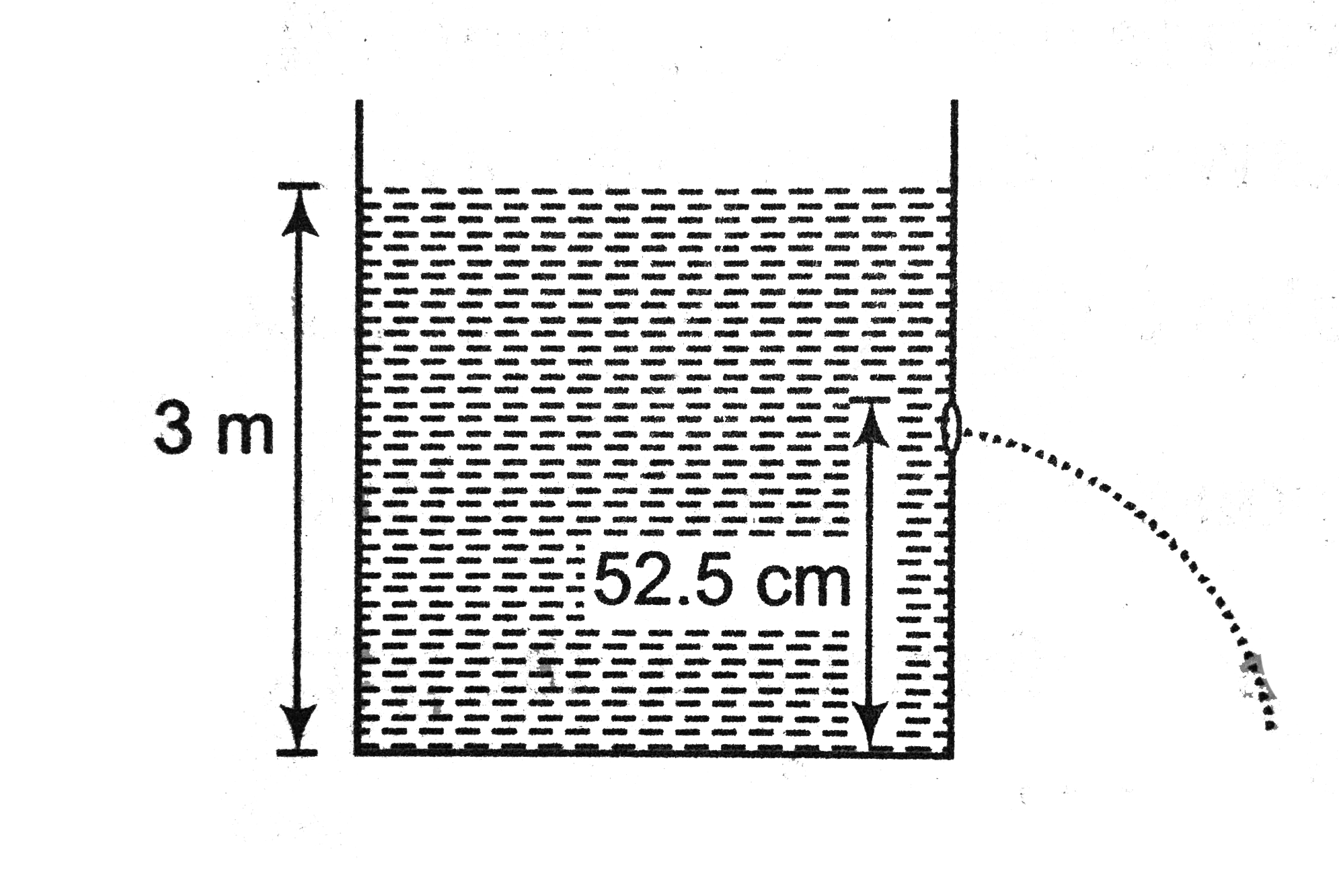
View SolutionA cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the tiome required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View Solution
Knowledge Check
What is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2A cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
A50m2/s2B40m2/s2C51.5m2/s2D50.5m2/s2A cylindrical tank is filled with water to a level of 4 m. A hole is opened at a height of 60 cm from bottom. The ratio of the area of the hole to that at cross-sectinal area at cylinder is 0.2. Then the velocity with which water is coming out is (g=10m/s2)
A7.9m/sB9.2m/sC8.4m/sD8.9m/s
At the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionOil is filled in a cylindrical container up to height 4m. A small hole of area 'p' is punched in the wall of the container at a height 1.52m from the bottom. The cross sectional area of the container is Q. Ifpq=0.1 then v is (where vis the velocity of oil coming out of the hole)
View Solution
An ideal liquid of density ρ is filled in a horizontally fixed syringe fitted with a piston. There is no friction between the piston and the inner surface of the syringe. Cross-sectional area of the syringe is A. At one end of the syringe, an orifice is made. When the piston is pushed into the syringe, the liquid comes out of the orifice and then following a parabolic path falls on the ground.
With what velocity does the liquid come out of the orifice?
View Solution
