The mass of the liquid flowing per second per unit area of cross-section of the tube is proportional to (pressure difference across the ends)^(n) and (average velocity of the liquid)^(m) . Which of the following relations between m and n is correct?
m=n
m=−n
m2=n
m=−n2
The correct Answer is:B
Let M=pnvm
ML−2T−1=(ML−1T−2)n(LT−1)m
=MnL−n+mT−2n−m
∴ n=1,−n+m=−2
∴ m=−2+n=−2+1=−1 ∴ m=−n
Topper's Solved these Questions
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBook:DISHA PUBLICATIONChapter:PHYSICAL WORLD, UNITS AND MEASUREMENTSExercise:Exercise - 1 : Concept Builder (Topicwise)(Topic 3 : Dimensions of Physical Quantities)
Explore 22 Videos
- OSCILLATIONS Book:DISHA PUBLICATIONChapter:OSCILLATIONS Exercise:Exercise-2 : Concept Applicator
Explore 28 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:DISHA PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Exercise -2 : Concept Applicator
Explore 26 Videos
Similar Questions
The volume of a liquid flowing per second through a capillary tube under a constant pressure difference is directly proportional to the_________power of radius.
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View Solution
Knowledge Check
The mass of the liquid flowing per second per unit area of cross section of the tube is proportional to Pxandvy , where P is the pressure difference and v is the velocity , then the relation between x and Y is
Ax=yBx=−yCy2=xDy=−x2V is the volume of a liquid flowing per second through a capillary tube of length l and radius r, under a pressure difference (p). If the velocity (v), mass (M) and time (T) are taken as the fundamental quantities, then the dimensional formula for η in the relation V=πpr48ηl
A[MV−1]B[M1V−1T−2]C[M1V1T−2]D[M1V−1T−1]The rate of flow Q (volume of liquid flowing per unit time) through a pipe depends on radius r, length L of pipe, pressure difference p across the ends of pipe and coefficient of viscosity of liquid η as Q∝rapbηcLd, then
Aa=4,b=1,c=−1,d=−1Ba=4,b=−1,c=1,d=−1Ca=4,b=1,c=1,d=−1Dvalues of a,b,c ang d cannot be detemind
A non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
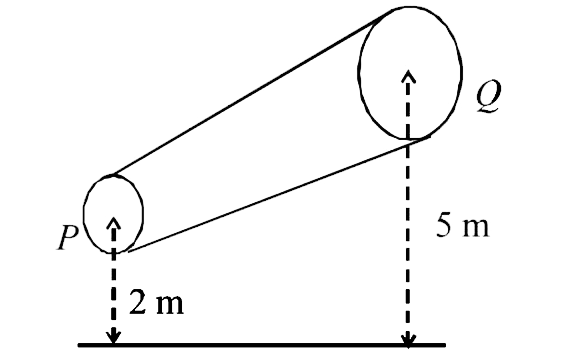
View SolutionA piot tube figure is mounted along the axis of a gas pipeline whose cross -sectional area is equal to S.

Assuming the viscosity to be negligible, find the volume of the gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquids and the gas are ρ0 and ρ respectively.
View SolutionA fluid is in streamline flow across a horizontal pipe of variable area of cross section. For this which of the following statements is correct?
View SolutionWhen a liquid moves steadily under come pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the exds of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and rare the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
Which of the following is correct:
View SolutionPoiseuille's's law for the flow of a liquid in a capillary tube is given by
η=πΔPa48LV
where η = co-efficient of viscosity of a liquid ΔP = Pressure difference across a length (L) of a tube of radius (a)
and V = Volume of the liquid flowing per second The maximum error that enters the calculations of η is due to the measurement of
View Solution