In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.(i) If x⊂A and A⊂B , then x⊂B(ii) If A⊂B and B⊂C then A⊂C
1) x is a element
A is a set
B is a set of sets
So, it is false
2) A and B is set
C is a set of sets
So, it is false
Topper's Solved these Questions
Similar Questions
In each of the following determine whether the statement is true or false. If it is true prove it . if it is false, give an example:

View SolutionIn each of the following determine whether the statement is true or false. If it is true prove it . if it is false, give an example: If x∈A and A∈B, then x∈B.
View Solution
Knowledge Check
If A⊂B, then A∪B=?
AϕBACBDNone of theseIf A⊂B and A≠B, then
AA is called a proper subset of BBA is called a super set of BCA is not a subset of BDB is a subset of A
In each of the following determine whether the statement is true or false. If it is true prove it . if it is false, give an example:
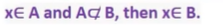
View SolutionIn each of the following determine whether the statement is true or false. If it is true prove it . if it is false, give an example: If A⊂B and B∈C, then A∈C.
View SolutionIn each of the following determine whether the statement is true or false. If it is true prove it . if it is false, give an example: If A⊂B and x∉B, then x∉A.
View SolutionIn each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.(i) If x⊂A and A⊂B , then x⊂B(ii) If A⊂B and B⊂C then A⊂C
View SolutionIn each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example
(i) If x∈AandA∈B, then x∈B
(ii) If A⊂BandB∈C, then A∈C
(iii) If A⊂BandB⊂C, then A⊂C
(iv) If A cancel(sub)B and B cancel(sub) C, then A cancel(sub)C
(v) If x in A and A cancel(sub)B, then x∈B
(vi) If A sub B and x cancel(in) B, then x cancel(in)A.
View SolutionIf A⊂B, then A∩B=?
View Solution
