If C and D are the points of internal and external division of line segment AB in the same ratio, then AC,AB, AD are in
AP
GP
HP
AGP
The correct Answer is:V
To solve the problem of finding the relationship between the lengths AC, AB, and AD when points C and D divide the line segment AB in the same ratio, we can follow these steps:
1. Define Points A and B:
Let point A be at the origin (0, 0) and point B be at (1, 0). This simplifies our calculations.
2. Ratio of Division:
Let the ratio in which point C divides AB be λ:1 (internal division). Therefore, the coordinates of point C can be calculated using the section formula:
C=(λ⋅xB+1⋅xAλ+1,λ⋅yB+1⋅yAλ+1)
Substituting the coordinates of A and B:
C=(λ⋅1+1⋅0λ+1,λ⋅0+1⋅0λ+1)=(λλ+1,0)
3. External Division:
For point D, which divides AB externally in the same ratio λ:1, we use the external division formula:
D=(λ⋅xB−1⋅xAλ−1,λ⋅yB−1⋅yAλ−1)
Substituting the coordinates of A and B:
D=(λ⋅1−1⋅0λ−1,λ⋅0−1⋅0λ−1)=(λλ−1,0)
4. Calculate Distances:
- Distance AC:
AC=|C−A|=∣∣∣λλ+1−0∣∣∣=λλ+1
- Distance AB:
AB=|B−A|=|1−0|=1
- Distance AD:
AD=|D−A|=∣∣∣λλ−1−0∣∣∣=λλ−1
5. Establish the Relationship:
Now we can express the ratios:
- The ratio ACAB=λλ+11=λλ+1
- The ratio ADAB=λλ−11=λλ−1
6. Conclusion:
Since both AC and AD are expressed in terms of λ, we can conclude that:
AC:AB:AD=λλ+1:1:λλ−1
Let point A be at the origin (0, 0) and point B be at (1, 0). This simplifies our calculations.
Let the ratio in which point C divides AB be λ:1 (internal division). Therefore, the coordinates of point C can be calculated using the section formula:
C=(λ⋅xB+1⋅xAλ+1,λ⋅yB+1⋅yAλ+1)
Substituting the coordinates of A and B:
C=(λ⋅1+1⋅0λ+1,λ⋅0+1⋅0λ+1)=(λλ+1,0)
For point D, which divides AB externally in the same ratio λ:1, we use the external division formula:
D=(λ⋅xB−1⋅xAλ−1,λ⋅yB−1⋅yAλ−1)
Substituting the coordinates of A and B:
D=(λ⋅1−1⋅0λ−1,λ⋅0−1⋅0λ−1)=(λλ−1,0)
- Distance AC:
AC=|C−A|=∣∣∣λλ+1−0∣∣∣=λλ+1
- Distance AB:
AB=|B−A|=|1−0|=1
- Distance AD:
AD=|D−A|=∣∣∣λλ−1−0∣∣∣=λλ−1
Now we can express the ratios:
- The ratio ACAB=λλ+11=λλ+1
- The ratio ADAB=λλ−11=λλ−1
Since both AC and AD are expressed in terms of λ, we can conclude that:
AC:AB:AD=λλ+1:1:λλ−1
Topper's Solved these Questions
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Section II - Assertion Reason Type
6 Videos
- BINOMIAL THEOREM AND ITS APPLCIATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test
60 Videos
- CONIC SECTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - CONIC SECTIONSEXERCISE - Section I - Solved Mcqs
1 Videos
Similar Questions
Knowledge Check
A point C is called the midpoint of a line segment ¯¯¯¯¯¯AB if
AC is an intrerior points of ABBAC =CBCC is an interior point of AB such that ¯¯¯¯¯¯AC=¯¯¯¯¯¯CBDAC+CB=ABIf position vectors of the points A, B and C are a, b and c respectively and the points D and E divides line segment AC and AB in the ratio 2:1 and 1:3, respectively. Then, the points of intersection of BD and EC divides EC in the ratio
A2:1B1:3C1:2D3:2On the circle with centre O, points A, B are such that OA =AB. A point C is located on the tangent at B to the circle such that A and C are on the opposite sides of the line OB and Ab =BC. The line segment AC intersects the circle again at F. Then the ratio ∠BOF:∠BOC is equal to-
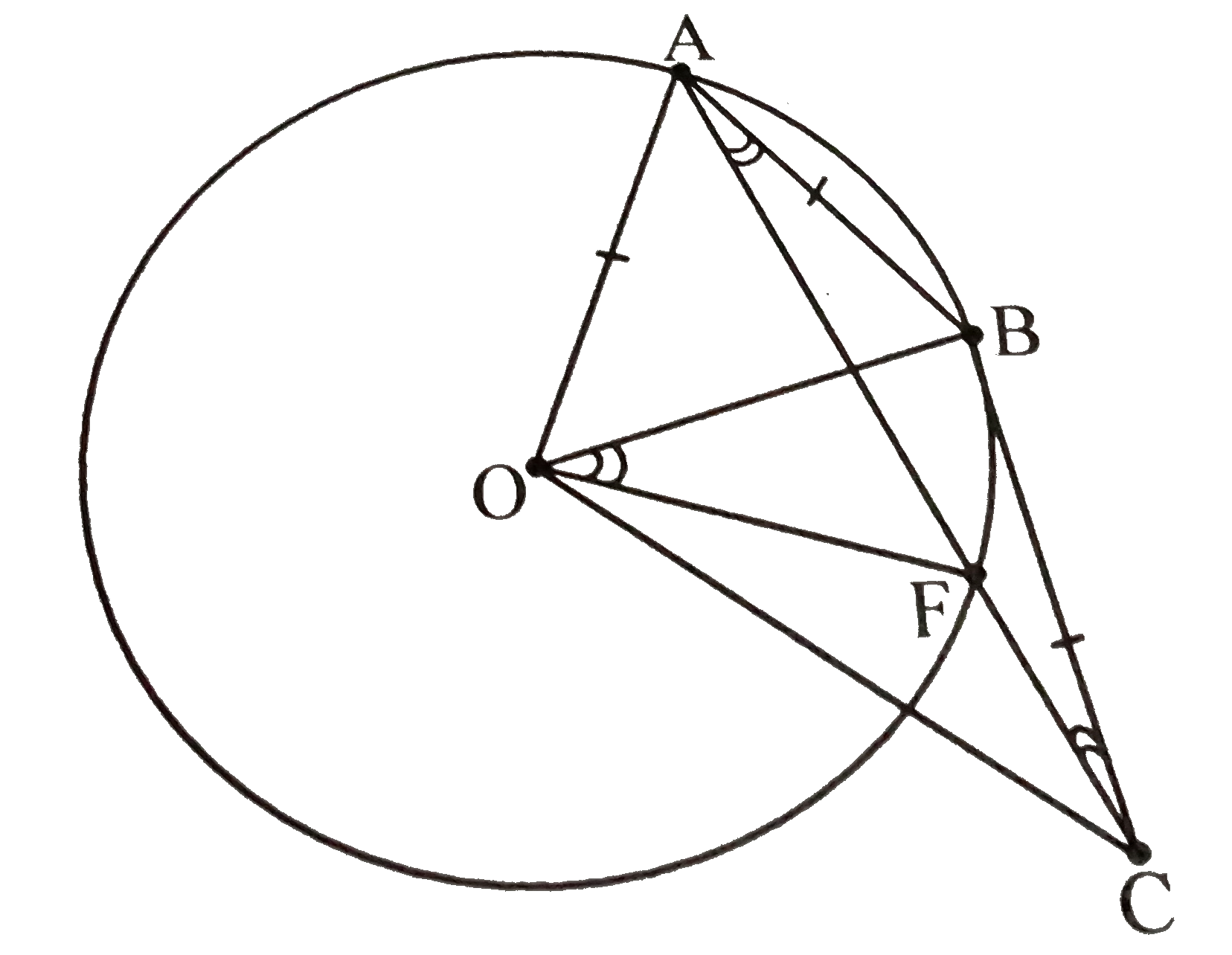 A1:2B2:3C3:4D4:5
A1:2B2:3C3:4D4:5
If A. B and C are three points on a line, and B lies between A and C then prove that AB−BC=AC.
View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BE
View SolutionDraw a line segment of length 8 cm and divides it in the ratio 2:3
View Solution. Find the coordinates of the points which divide, internally and externally, the line joining the point (a+b,a−b) to the point (a−b,a+b) in the ratio a:b.
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View Solution

