Let O(0,0), P(3,4) and Q(6,0) be the vertices of triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are
(43,3)
(3,23)
(3,43)
(43,23)
The correct Answer is:C
Clearly, ΔOPQ is an isoscles triangle with OP=PQ. So, point R must coincide with the centroid of ΔOPQ.
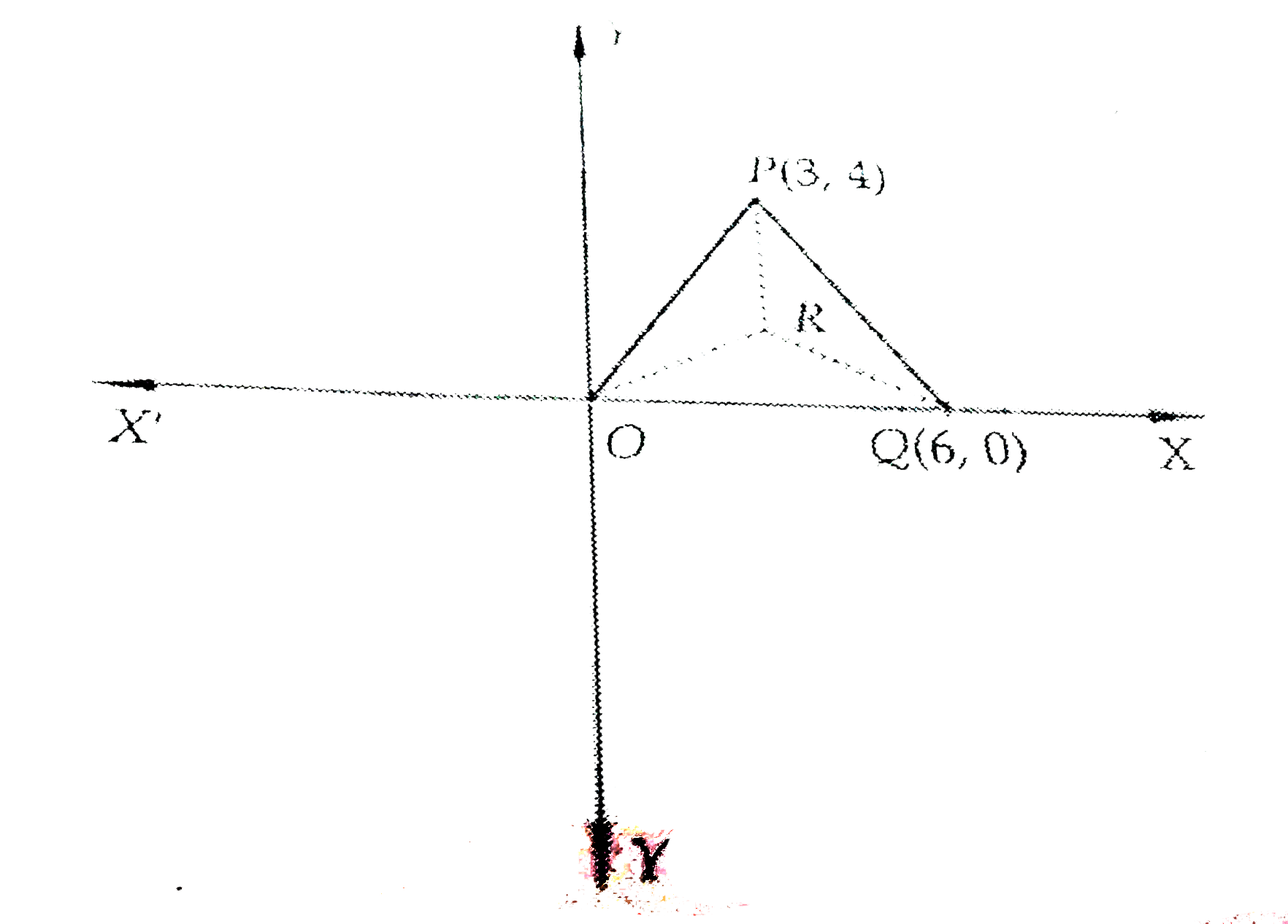
Hence, the coordinates of R are (0+6+33,0+0+43)=(3,43)
Topper's Solved these Questions
- CARTESIAN CO-ORDINATE SYSTEM Book:OBJECTIVE RD SHARMAChapter:CARTESIAN CO-ORDINATE SYSTEM Exercise:Section II - Assertion Reason Type
Explore 6 Videos
- CARTESIAN CO-ORDINATE SYSTEM Book:OBJECTIVE RD SHARMAChapter:CARTESIAN CO-ORDINATE SYSTEM Exercise:Exercise
Explore 29 Videos
- CARTESIAN CO-ORDINATE SYSTEM Book:OBJECTIVE RD SHARMAChapter:CARTESIAN CO-ORDINATE SYSTEM Exercise:Exercise
Explore 29 Videos
- BINOMIAL THEOREM AND ITS APPLCIATIONS Book:OBJECTIVE RD SHARMAChapter:BINOMIAL THEOREM AND ITS APPLCIATIONS Exercise:Chapter Test
Explore 60 Videos
- CONIC SECTIONSBook:OBJECTIVE RD SHARMAChapter:CONIC SECTIONSExercise:Section I - Solved Mcqs
Explore 1 Video
Similar Questions
Let O (0,0),P(3,4),Q(6,0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are
View SolutionLet O(0, 0), P(3, 4), Q(6, 0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR, PQR are of equal area. The coordinates of R are
View Solution
Knowledge Check
Let O(0, 0), P(3, 4), Q(6, 0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR, PQR are of equal area. The coordinates of R are
A(43,3)B(3,23)C(3,43)D(43,23)The points P(0, 6), Q(-5, 3) and R(3, 1) are the vertices of a triangle which is
AequilateralBisoscelesCscaleneDright angledLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then ∠A equals -
A30∘B60∘C90∘D120∘
The triangle PQR of which the angles P,Q,R satisfy cos P =sinQ2sinR is :
View SolutionP(6, 3, 2), Q(5, 1, 3)andR(3, 3, 5) are three vertices of a triangle P Q R. Find ∠P Q R.
View SolutionIn a triangle PQR , let ∠PQR=30o and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE? ∠QPR=45o (b) The area of the triangle PQR is 25√3 and ∠QRP=120o (c) The radius of the incircle of the triangle PQR is 10√3−15 (d) The area of the circumcircle of the triangle PQR is 100 π
View SolutionABC is a triangle. Forces P, Q, R acting along the lines OA, OB and OC are in equilibrium. Then P:Q:R= …..
If O is the orthocentre of the triangle ABC
View SolutionABC is a triangle. Forces P, Q, R acting along the lines OA, OB and OC are in equilibrium. Then P:Q:R= …..
If O is the incentre of ΔABC
View Solution