A simple barometer tube contains some air in it. The length of the tube above the mercury level in the trough is 80 cm. The height of mercury in the tube is 71 cm at normal atmospheric pressure. What is the actual decrease in the atmospheric pressure if the barometer reads 65 cm ?
Find the length of the tube above the nercury level in the trough and height of Hg in the tube normal atmosphere pressure (Pa)
Is the given barometer tube contains air in it ?
Then, Is Pa= Pressure due to entrapped air (P1) and the height of Hg column ? (1)
Take area of cross section of the tube as 'a'.
Get the value of 'P1' from (1)
Find the volume of entrapped air in the tube. Take in the tube. Take it as 'V1'.
If barometer reads 65 cm of Hg column, then the atmosphere pressure (Pa1) is equal to 65 cm of Hg + pressure due to air entrapped in the tube (P2).
i.e., P1a=65cm+P2 (2)
Now, find the volume of the air entrapped in the barometer tube.
Take it as 'V2'.
Find the value of P2 by using Boyle's law.
i.e., P1V1=P2V2
⇒P2=P1V1V2 (3) Substitute the value of 'P2' in (2) and find the value of P1a.
Then, actual decrease in atmospheric pressure will be equal to (Pa−P1a).
Topper's Solved these Questions
- HYDROSTATICEBook:PEARSON IIT JEE FOUNDATIONChapter:HYDROSTATICEExercise:LEVEL 2 UNDERSTANDING BASED QUESTION
Explore 6 Videos
- HYDROSTATICEBook:PEARSON IIT JEE FOUNDATIONChapter:HYDROSTATICEExercise:LEVEL 3
Explore 5 Videos
- HYDROSTATICEBook:PEARSON IIT JEE FOUNDATIONChapter:HYDROSTATICEExercise:LEVEL 1 MULTIPLE CHOICE QUESTIONS
Explore 29 Videos
- HEATBook:PEARSON IIT JEE FOUNDATIONChapter:HEATExercise:All Questions
Explore 115 Videos
- LIGHTBook:PEARSON IIT JEE FOUNDATIONChapter:LIGHTExercise:Level 3
Explore 10 Videos
Similar Questions
Knowledge Check
Suppose the pressure at the surface of mercury in as barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
AP1=0,P2= atgmospheric pressureBP1= atmosphereic pressure P2=0CP1=P2=atmospheric pressureDP1=P2=0The atmoshperic pressure at sea level is determined by what height of mercury comlumn in a barometer?
A76 cmB7.6 cmC86 cmD8.6 cmA vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
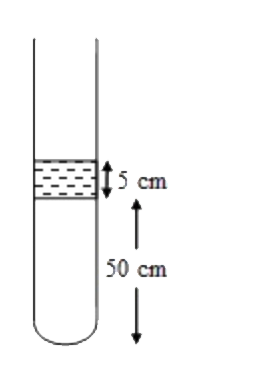 A56 cmB57 cmC60 cmD50 cm
A56 cmB57 cmC60 cmD50 cm
A glass tube sealed at one end and containing a quantity of air is immersed in mercury until the sealed end is 10 cm from the surface of mercury. At 0∘C the level of mercury in the tube is 5 cm above the level of mercury in the vessel. The length of the tube is 15 cm. To what temperature should the air in the tube be raised as to fill the tube completely? The atmospheric pressure is 75 cm of Hg. Neglect any change in the level of mercury in the vessel.
View SolutionA faulty barometer tube is 90cm long and its contains some air above mercury. The reading is cm when the true atmospheric pressure 76cm. What will be the true atmospheric pressure if the reading on this barometer is 74 cm? (H = 10cm of water column)
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionA mercury barometer reads 75cm in vertical position . If the tube is inclined by 60∘ to the vertical, the length of the mercury in the tube will be
View SolutionWhat will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
View Solution
