What will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle with the vertical direction ?
x
The correct Answer is:B
To find the length of the mercury column in a barometer tube inclined at an angle ϕ with the vertical when the atmospheric pressure is x cm of mercury, we can follow these steps:
1. Understanding the Setup:
- We have a barometer tube that is inclined at an angle ϕ with respect to the vertical.
- The height of the mercury column due to atmospheric pressure is x cm.
2. Identifying the Components:
- When the tube is inclined, the length of the mercury column L can be related to the vertical height of the mercury column. The vertical height of the mercury column is x cm.
3. Using Trigonometry:
- In the inclined position, we can use trigonometric relationships. The vertical height x can be expressed in terms of the length L of the mercury column and the angle ϕ:
x=Lcos(ϕ)
- Here, L is the hypotenuse (the length of the mercury column) and x is the adjacent side (the vertical height of the mercury column).
4. Solving for Length L:
- Rearranging the equation gives:
L=xcos(ϕ)
- This can also be expressed as:
L=xsec(ϕ)
5. Conclusion:
- Therefore, the length of the mercury column in the barometer tube when inclined at an angle ϕ with the vertical is:
L=xsec(ϕ)
Final Answer:
The length of the mercury column in the barometer tube is L=xsec(ϕ).
- We have a barometer tube that is inclined at an angle ϕ with respect to the vertical.
- The height of the mercury column due to atmospheric pressure is x cm.
- When the tube is inclined, the length of the mercury column L can be related to the vertical height of the mercury column. The vertical height of the mercury column is x cm.
- In the inclined position, we can use trigonometric relationships. The vertical height x can be expressed in terms of the length L of the mercury column and the angle ϕ:
x=Lcos(ϕ)
- Here, L is the hypotenuse (the length of the mercury column) and x is the adjacent side (the vertical height of the mercury column).
- Rearranging the equation gives:
L=xcos(ϕ)
- This can also be expressed as:
L=xsec(ϕ)
- Therefore, the length of the mercury column in the barometer tube when inclined at an angle ϕ with the vertical is:
L=xsec(ϕ)
The length of the mercury column in the barometer tube is L=xsec(ϕ).
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Check point 13.2
Explore 10 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Check point 13.3
Explore 10 Videos
- FLUID MECHANICSBook:DC PANDEYChapter:FLUID MECHANICSExercise:Example 13.35
Explore 1 Video
- EXPERIMENTSBook:DC PANDEYChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
What will be the length of mercury column in a barometer tube when the atmosperic pressure is 75cm of mercury and the tube is inclined at an angle of 60∘ with the horizontal direction?
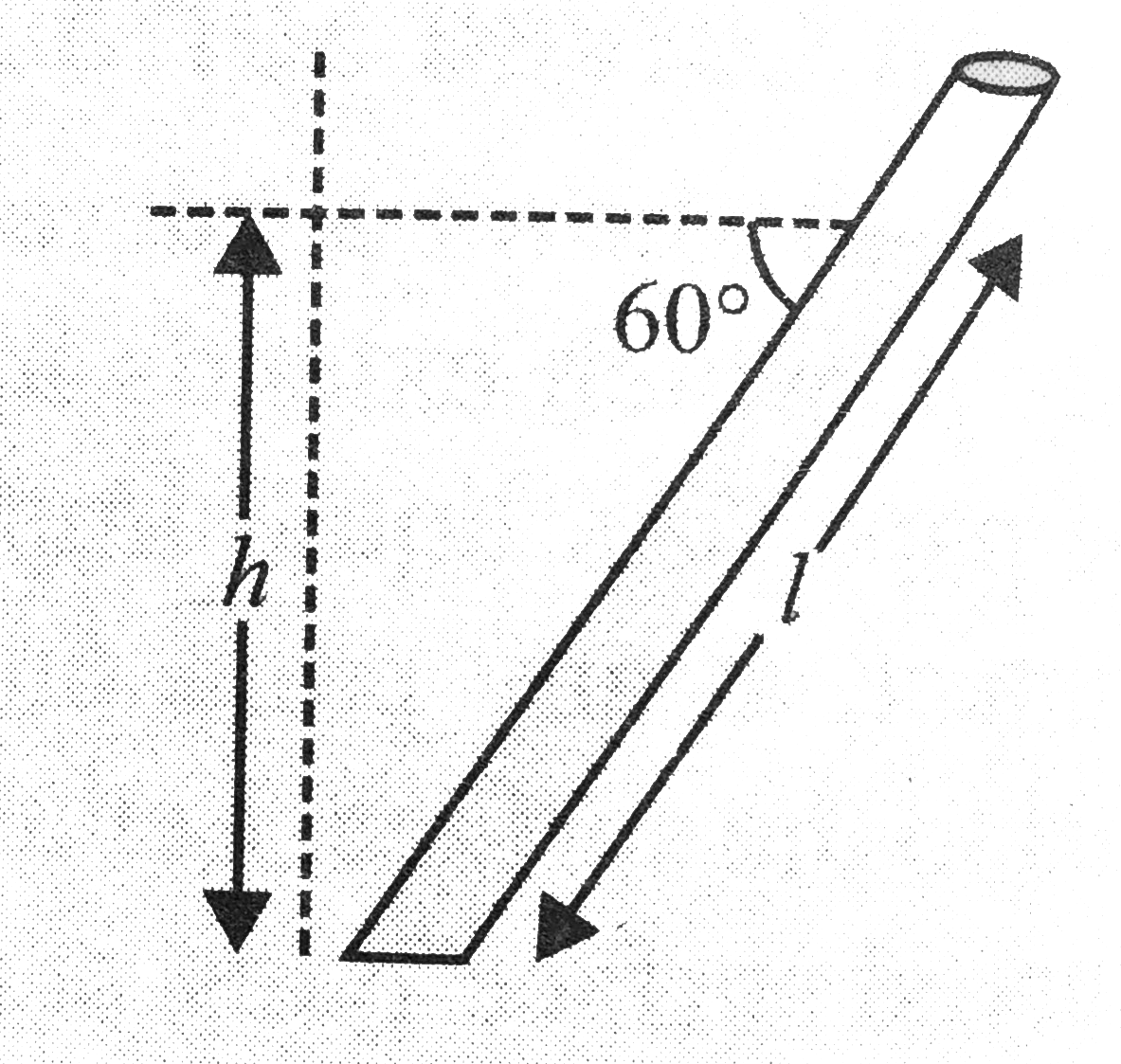
View SolutionWhat will be the length of mercury column in a barometer tube, when the atmospheric pressure is 76 cm of mercury and the tube is inclined at an angle of 30∘ with the horizontal direction ?
View Solution
Knowledge Check
Suppose the pressure at the surface of mercury in as barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
AP1=0,P2= atgmospheric pressureBP1= atmosphereic pressure P2=0CP1=P2=atmospheric pressureDP1=P2=0
What will be the height of mercury column in a barometer it it is taken to the moon?
View SolutionWhy mercury is used in barometer for measuring atmospheric pressure?
View SolutionWhat will happen if water is used in place of mercury in a barometer tube?
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionIf the length of the mercury column in a mercury barometer is 76 cm, what is the equivalent height of the water column ?
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
View SolutionA barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass135∘ and surface tension of mercury =0.465Nm−1. Density of mercury=13600kgm−3.
View Solution

