Using the relation 2(1−cosx)<x2,x≠0 or otherwise, prove that s∈(tanx)≥x,∀x∈[0,π4].
Video Solution
Text Solution
Let f(x)=sin(tanx)−x
f'(x)=cos(tanx)⋅sec2x−1
=cos(tanx)(1+tan2x)−1
=tan2x{cos(tanx)}+cos(tanx)−1
>tan2xcos(tanx)−tan2x2
⎡⎢⎣∵2(1−cosx)<x2x≠0⇒cosx>1−x22⇒ cos(tanx)>1−tan2x2⎤⎥⎦
f'(x)>tan2x[cos(tanx)−cos(π/3)]>0
⇒f(x) is increasing function, for all x∈[0,π/4]
⇒ sin(tanx)≥x
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:ROLLES AND LAGRANGES THEOREM (OBJECTIVE QUESTIONS I)
Explore 1 Video
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:ROLLES AND LAGRANGES THEOREM (ASSERTION AND REASON )
Explore 1 Video
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:RATE MEASURE, INCREASING AND DECREASING FUNCTIONS (MATCH THE COLUMNS )
Explore 4 Videos
- 3D GeometryBook:IIT JEE PREVIOUS YEARChapter:3D GeometryExercise:Equation of Plane Objective Question II (Integer Answer Type Question)
Explore 1 Video
- AREABook:IIT JEE PREVIOUS YEARChapter:AREAExercise:AREA USING INTEGRATION
Explore 55 Videos
Similar Questions
Knowledge Check
If x1,x2,...,xn are real numbers, then the largest value of the expression
sinx1cosx2+sinx2cosx3+...+sinxncosx1, isAnBn2Cn4D√n2−1
Using constraint method find the relation between accelerations of 1 and 2.
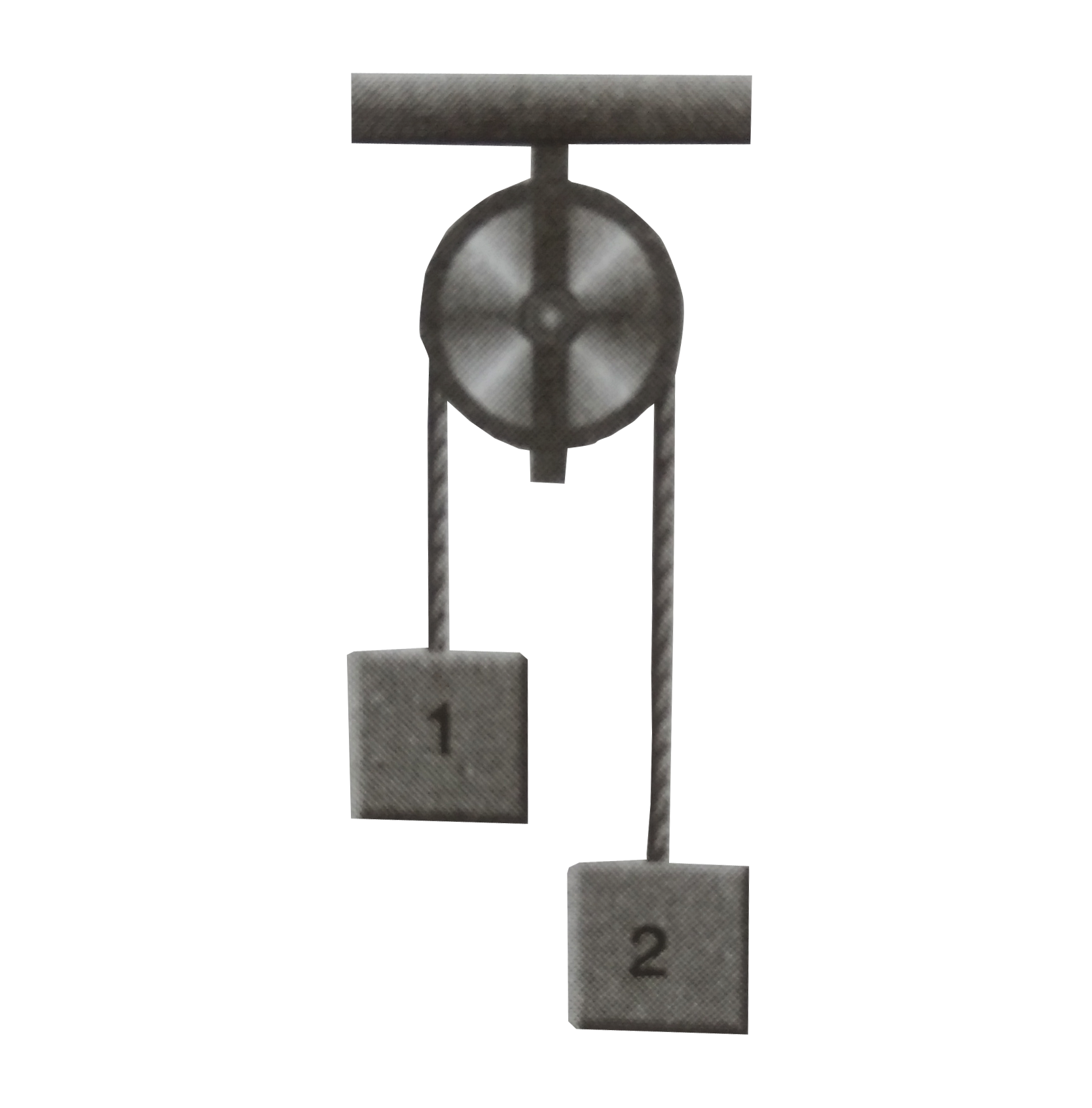
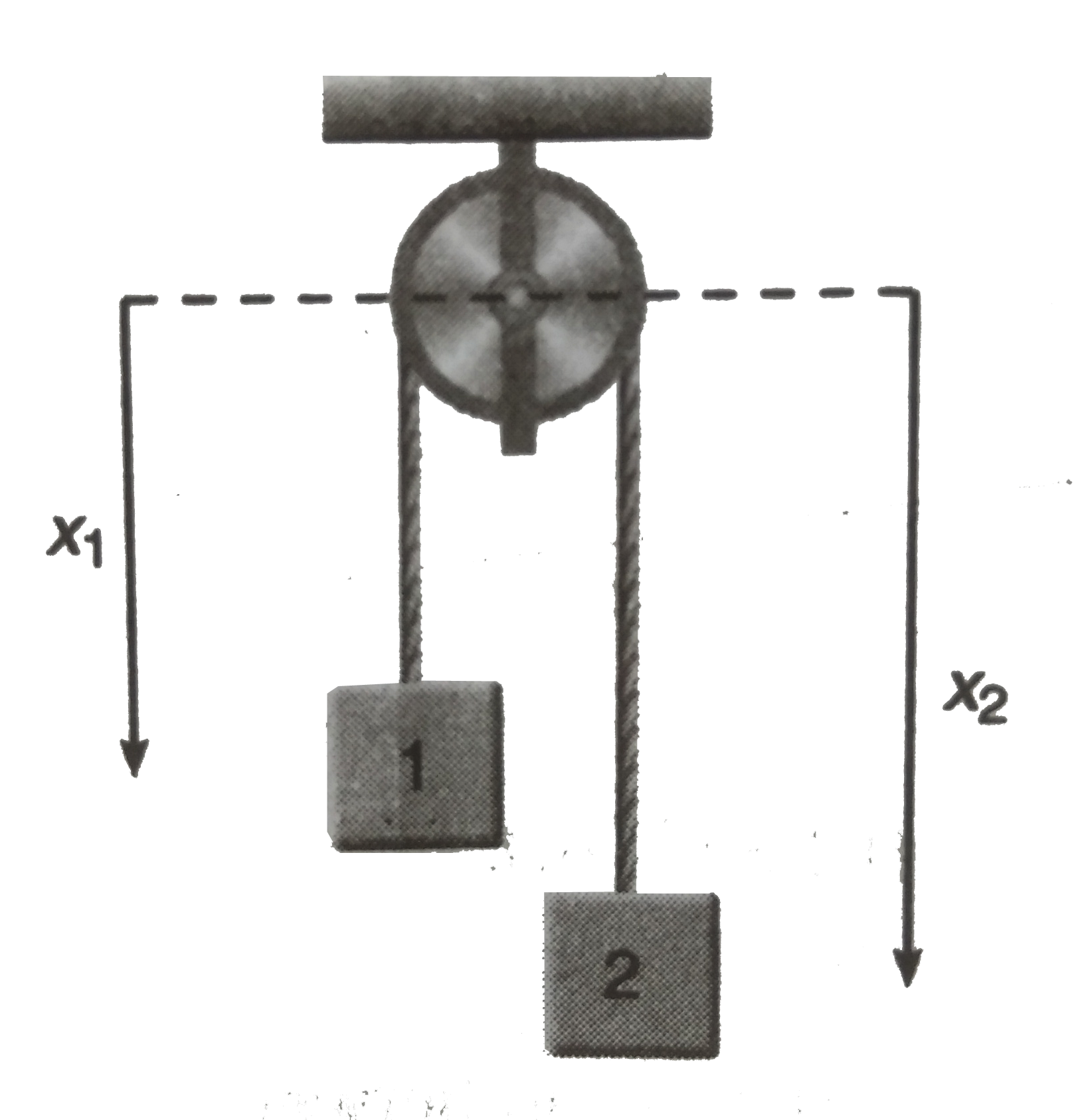
View SolutionUsing constraint method find the relation between of a1 and a2.

View SolutionFind the derivative of the following :
1−cosx1+cosx.
View SolutionFind the differentiation of y=tan−1 ⎷1+cosx21−cosx2
View SolutionUsing contraint equation. Find the relation between a1anda2.
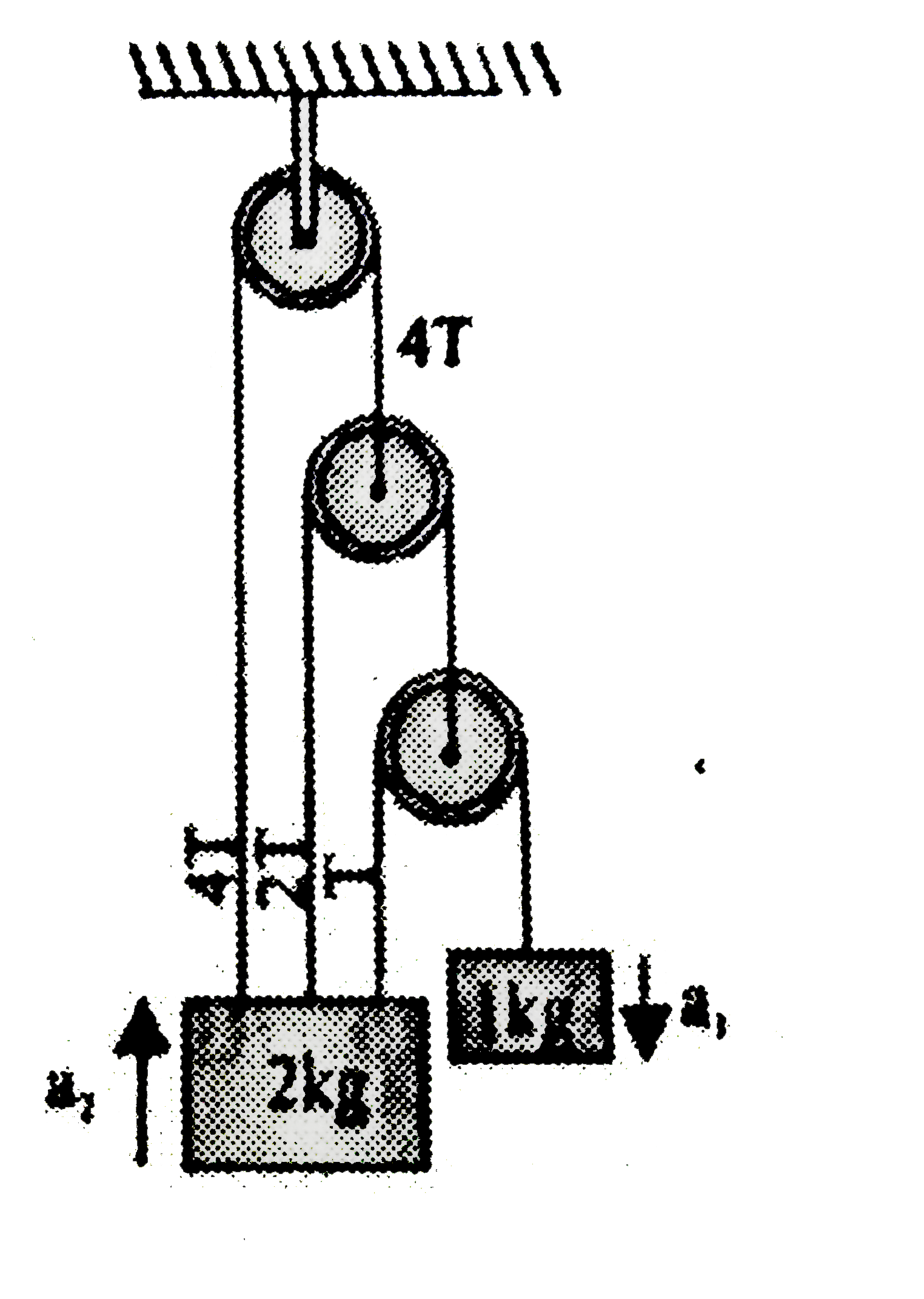
View Solution∫sin2x(1+cosx)2dx
View Solution∫sin2x(1+cosx)2dx
View Solution