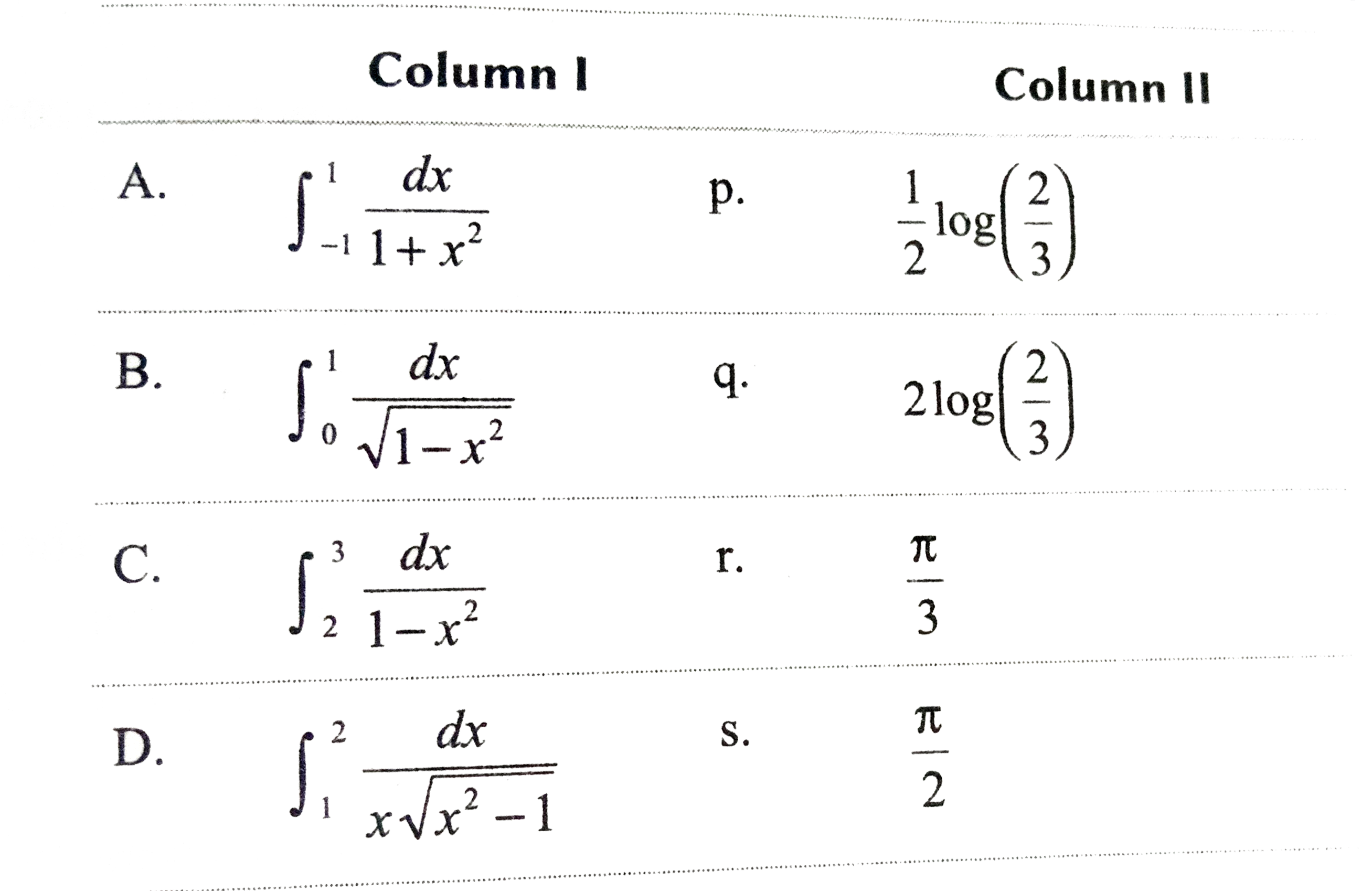
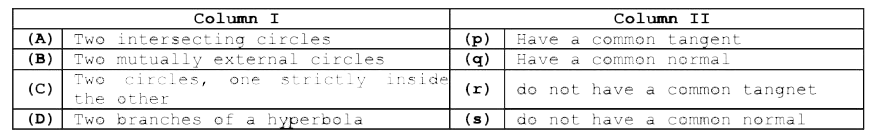Match the conditions/ expressions in Column I with statements in Column II.
Let the functions defined in Column I have domain (−π/2,π/2).
(##41Y_SP_MATH_C10_E02_025_Q01.png" width="80%">
Video Solution
Text Solution
ddx(x+sinx)=1+cosx=2cos2x2>0for −π2<x<π2.
Therefore , x+sinx is increasing in the given interval.
Therefore, (A)→(p) is the answer.
Again ddx(sec)=secxtanx which is >0 for 0<x<π/2
and <0 for −π2<x<0
Therefore, secx is neither increasing nor decreasing in the given interval. Therefore, (B)→(r) is the answer.
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - RATE MEASURE, INCREASING AND DECREASING FUNCTIONS (ANALYTICAL & DESCRIPTIVE QUESTIONS)
7 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - ROLLES AND LAGRANGES THEOREM (OBJECTIVE QUESTIONS I)
1 Video
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - RATE MEASURE, INCREASING AND DECREASING FUNCTIONS (FILL IN THE BLANKS )
2 Videos
- 3D GeometryBOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)
1 Video
- AREABOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION
55 Videos
Similar Questions
Knowledge Check
Match the items in Column I with the relevant item in column II.
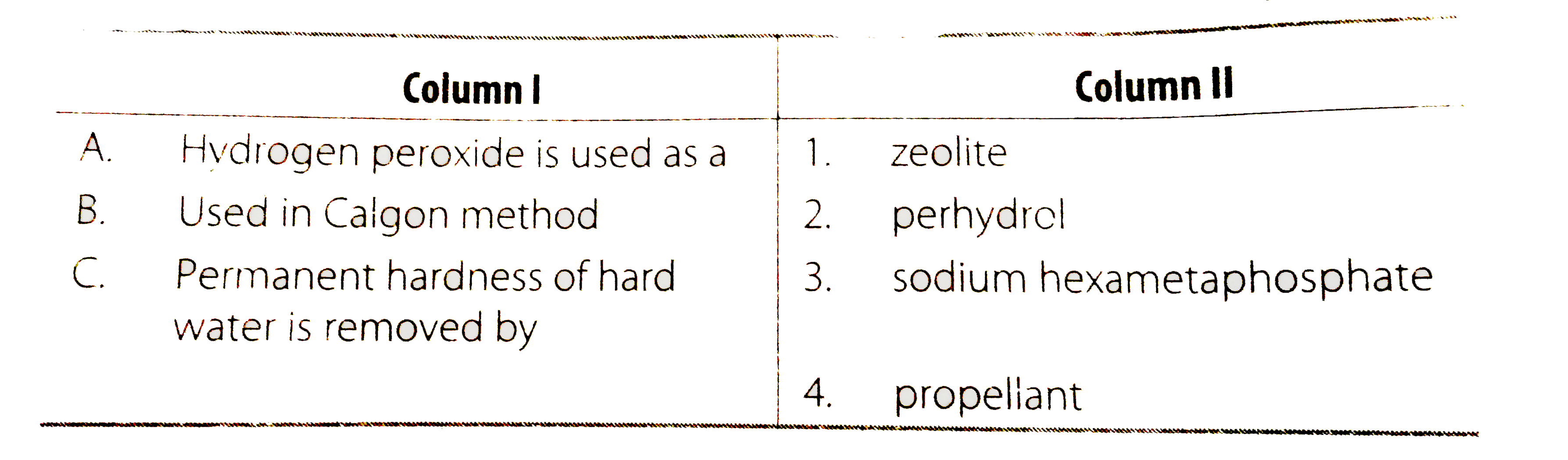 AP (p,r,s), Q(q, s), R(q,s), S(p, r, s)BP(p,r), Q(q), R(q, s), S(r,s)CP(p,s), Q(s), R(q), S(p, r, s)DP(p), Q(q ,s), R(s), S(p,s)
AP (p,r,s), Q(q, s), R(q,s), S(p, r, s)BP(p,r), Q(q), R(q, s), S(r,s)CP(p,s), Q(s), R(q), S(p, r, s)DP(p), Q(q ,s), R(s), S(p,s)Based on the above velocity-time graph for an object in motion along a straight line with constant acceleration, match the items in Column I with terms in Column II. Hence choose the correct options from the codes given below.
(##AHT_PGT_PHY_C02_E01_032_E01.png" width="80%">A B
B C
C D
D
match the column -I with column -II
(##FIITJEE_CHE_MB_05_C01_E06_003_Q01.png" width="80%">AP-1,Q-2,R-1.3 s-1.4BP-2,Q-3,R-1 s-4CP-2,Q-3,R-4 s-1DP-3,Q-4,R-2 s-1
Match the conditions /expression n Column I with statement in Column II (z≠0 is a complex number )

View SolutionLet the functions defined in Column I have domain (−π2,π2) and range (−∞,∞)
View SolutionMatch the conditions/expressions in Column I with statement in Column Ⅱ. (A). sin(π[x]) (B) sin{π(x−[x])}
View SolutionMatch the ColumnsMatch the conditions/expressions in Column I withstatement in Column II Let f(x)=x2−6x+5x2−5x+6.
View SolutionMatch the statement (A,B,C,D) in column I with the statement (p,q,r,s) in column II. The answers are to be properly bobbled.
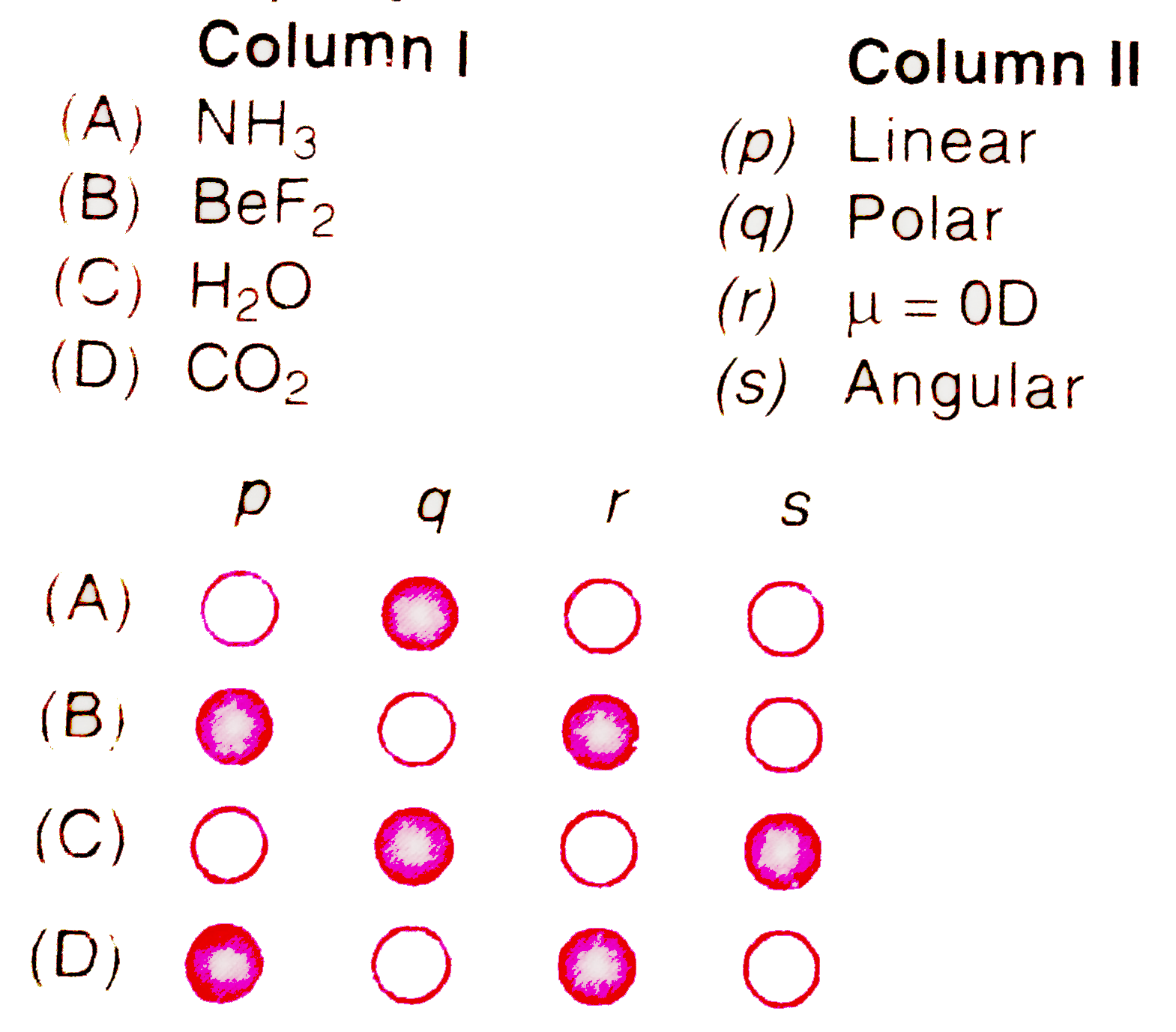
View Solution