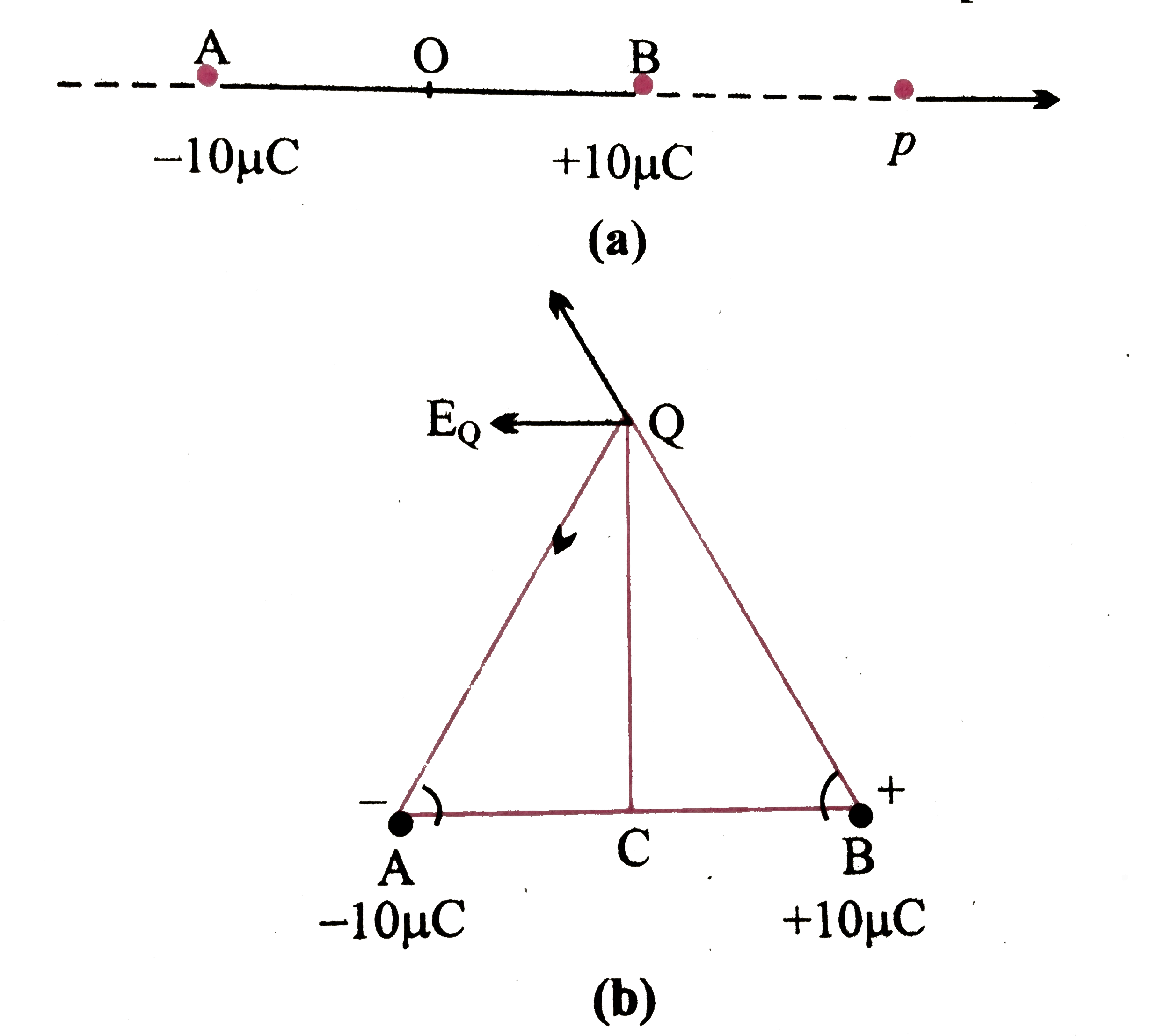
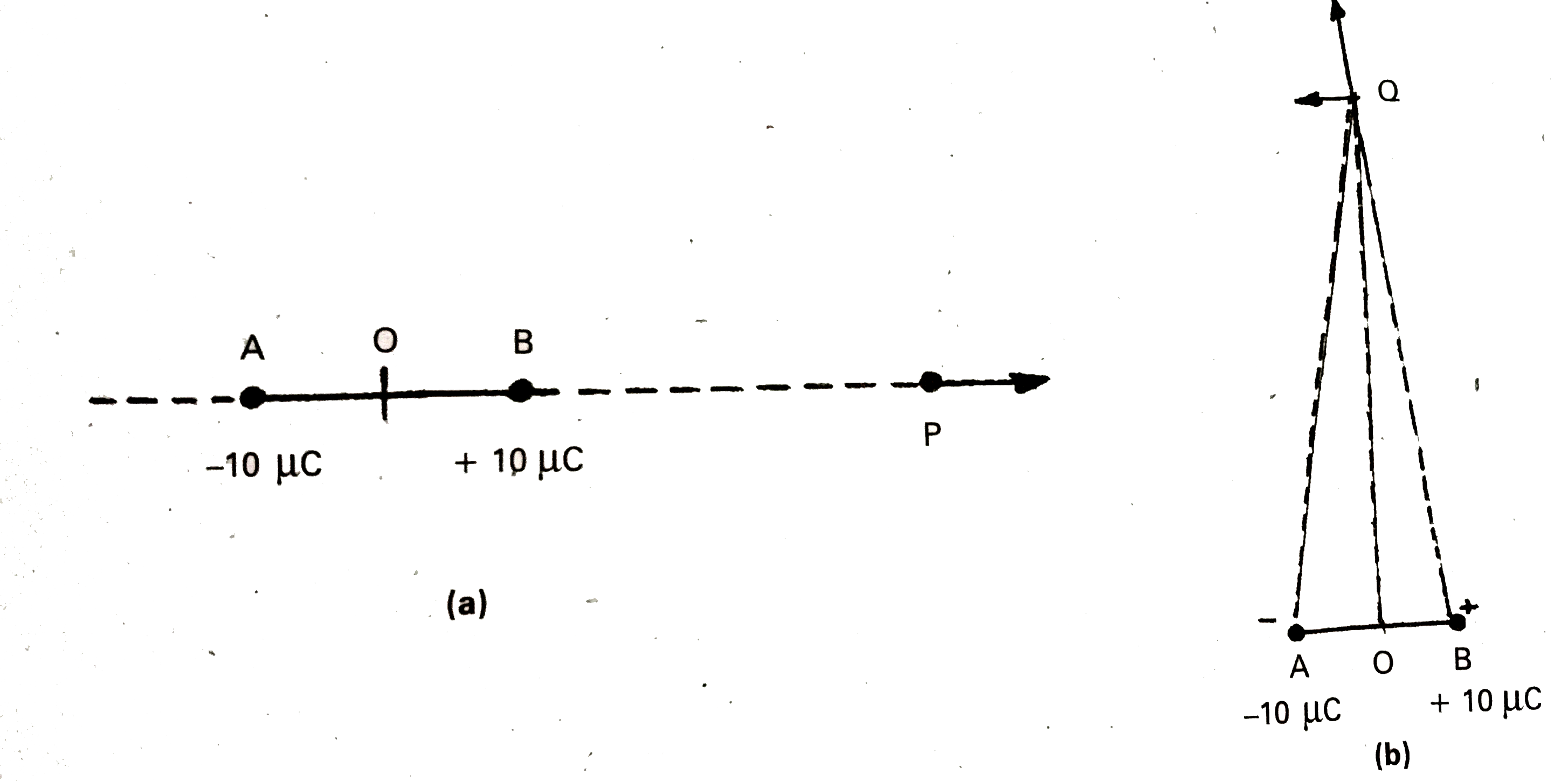
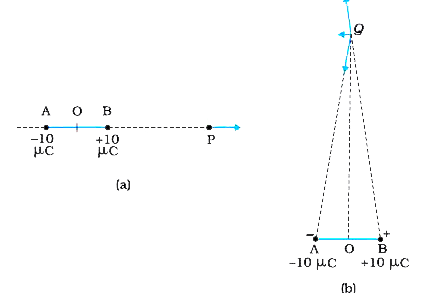
Two charges ±10μC are placed 5.0 mm apart. Determine the electric field at (a) a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charges, as shown in Fig. (a) and (b) be a point Q, 15 cm away from O on a line passing through O and normal to the axis of the dipole, as shown in Fig (b). 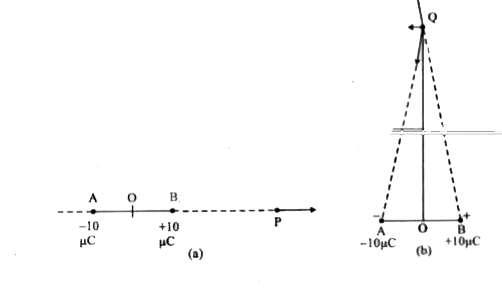Two charges pm 10 muC are placed 5.0 mm apart. Determine the electric field at (a) a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charges, as shown in Fig. (a) and (b) be a point Q, 15 cm away from O on a line passing through O and normal to the axis of the dipole, as shown in Fig (b). Solution in Tamil

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Field at P due to charge +10μC=10−54π(8.854×10−12)×1(15−0.25)2×10−4
=4.13×106NC−1 along BP
Field at P due to charge −10μC=10−54π(8.854×10−12)×1(15+0.25)2×10−4
The resultant electric field P due to the two charges at A and B is =2.7×105NC−1 along BP. In this example, the ratio OP/OB is quite large (= 60). Thus, we can expect to get approximately the same result as above by directly using the formula for electric field at a far-away point on the axis of a dipole.
For a dipole consisting of charges ±q, 2a distance apart, the electric field at a distance r from the centre on the axis of the dipole has a magnitude E=2p4πε0r3 when r>>a
where p=2a q is the magnitude of the dipole moment.
The direction of electric field on the dipole axis is always along the direction of the dipole moment vector (i.e., from -q to q). Here, p=10−5×5×10−3=5×10−8Cm
Therefore E=2×5×10−84π(8.854×10−12)×1(15)2×10−6=2.6×105NC−1
along the dipole moment direction AB, which is close to the result obtained earlier.
Field at Q due to charge +10μC at B =10−54π(8.851×10−12)×1[152+(0.25)2]×10−4
Field at Q due to charge −10μC at A=10−54π(8.854×10−12)×1[152+(0.25)2]×10−4
=3.99×106NC−1 along QA.
Clearly, the components of these two forces with equal magnitudes cancel along the direction OQ but add up along the direction parallel to BA. Therefore, the resultant electric field at due to the two charges at A and B is =2×0.25√152+(0.25)2×3.99×106 along BA=1.33×105NC−1 along BA.
As in (a), we can expect to get approximately the same result using the formula for dipole field at a point on the normal to the axis of the dipole.
When r>>a,E=p4πε0r3=5×10−84π(8.854×10−12)×1(15)3×10−8=1.33×105NC−1
The direction of electric field in this case in opposite to the direction of the dipole moment vector.

Updated on:21/07/2023
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions