Question

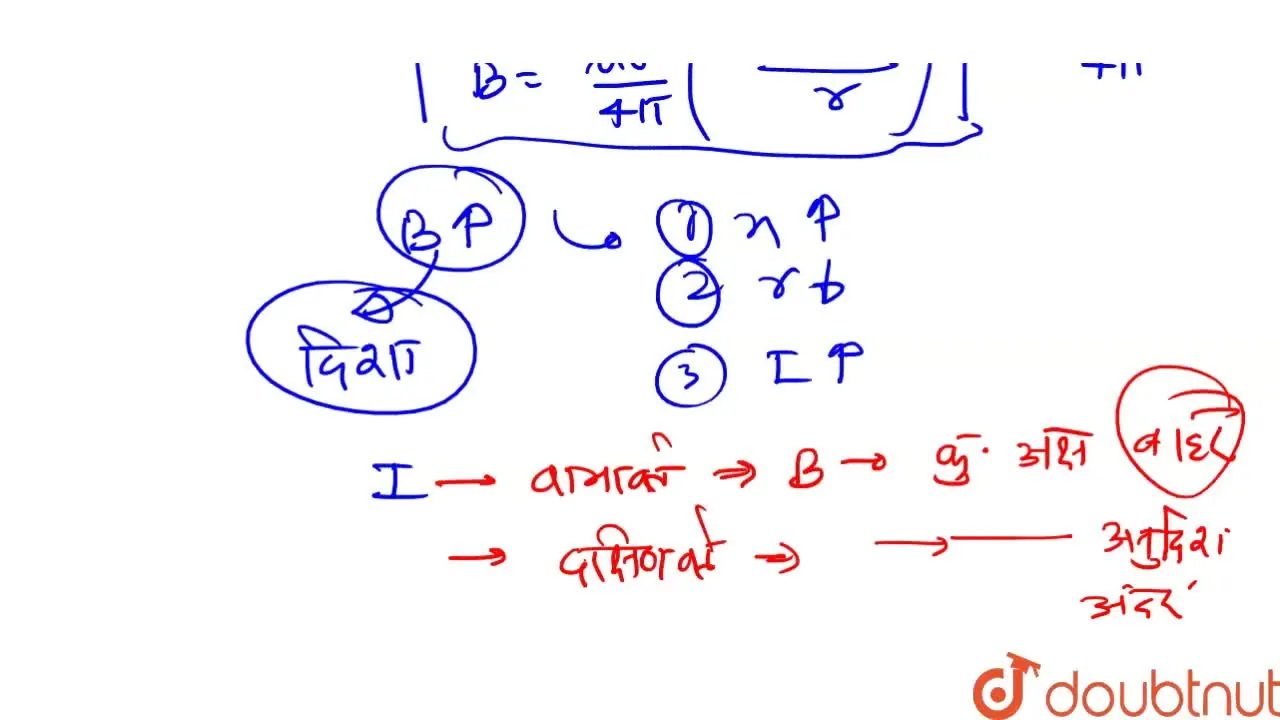
वायोट सावटे का नियम की व्याख्या करें । धारावाही वृत्ताकार कुंडली के केंद्र पर चुंबकीय क्षेत्र का व्यंजक प्राप्त करें ।

Explanation

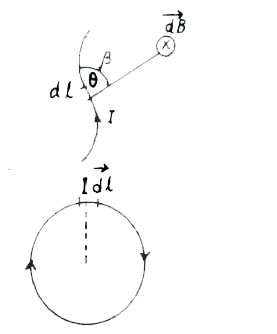
वायोट -सावर्ट का नियम- वायोट सावर्ट का नियम धारावाही चालक के कारण किसी बिंदु पर चुंबकीय क्षेत्र कि सामर्ध्य निर्धारित करता है। माना कि dl लम्बाई का AB अल्पांश है जिसमे धारा l प्रवाहित हो रही है। धारावाही अल्पांश के कारण r दुरी पर स्थित एक बिंदु P पर चुंबकीय क्षेत्र `vec(dB)` निम्न पर निर्भर करता है।
बायोट-सावर्ट के अनुसार `d B prop dl` ..(i)
`d B prop l` ..(ii) `d B prop sin theta` ...(iii) `d B prop (1)/(r^(2))` ...(iv)
समी (i), (ii), (iii), (iv) से `d B prop (l dl sin theta)/(r^(2)) :. d B= K (l dl sin theta)/(r^(2))`
जहाँ K नियतांक है, जिसका मान `K = (mu_(0))/(4pi)` होता है ।
अंत `dB= (mu_(0))/(4pi) . (l dl sin theta)/(r^(2))`
माना त्रिज्या a की धारावाही कुंडली में `l vec(dl)` धारावाही अल्पांश लिया गया। यह धारावाही `l vec(dl)` के कारण कुंडली के केंद्र पर चुंबकीय क्षेत्र `vec(dB) = (mu_(0))/(4pi) (l vec(dl) xx vec(r))/(r^(2))`
इस प्रकार `l vec(dl)` और `vec(r)` के मध्य में एकल कोण `90^(@)` है तथा r=a है।
सम्पूर्ण कुंडली के कारण कुंडली के केंद्र पर चुंबकीय क्षेत्र की समीकरण (i) के समाकलन द्वारा गणना की जाती है।
`oint dB= oint (M_(0))/(4pi) (ldl)/(a^(2))` या `N= (M_(0))/(4pi) (l)/(a^(2)) oint dl`
`dl = 2pi a, " " :. B= (mu_(0))/(4pi) (l)/(a^(2)) xx 2pi a` या `B= (mu_(0)l)/(2pi a)`