किसी गोलीय सतह से अपवर्तन के लिए सूत्र μ2v−μ1u=μ2−μ1r निकालें।
जब आभासी प्रतिबिम्ब बन रहा हो-माना एक बिन्दुवत वस्तु O विरल माध्यम (n1) में गोलीय उत्तल सतह के मुख्य अक्ष पर स्थित है । बिम्ब O से प्रकाश की एक किरण उत्तल पर A पर आपतित होती है । अपवर्तन के पश्चात्, यह अभिलम्ब AC की तरफ मुड जाता है और AB के अनुदिश गति करती है।
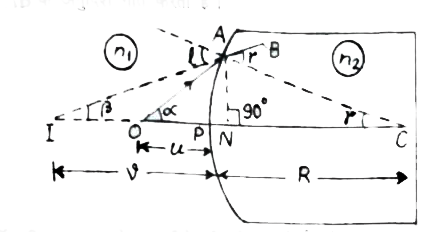
अपवर्तित किरण AB को जब पीछे की ओर बढ़ाते है , तो यह मुख्य अक्ष को बिंदु I पर मिलती है।
चूँकि गोलीय पृष्ठ का द्वारक छोटा है (माना ) अतः बिंदु N बिंदु P में बहुत निकट होगा।
NO = PO , NC=PC, NI = PI
अतः समीकरण (viii ) तथा (ix ) को इस प्रकार भी लिखा जा सकता है ,
i=ANPO+ANPC..(x)
r=ANPI+ANPC..(xi)
स्नेल के नियम के अनुसार , sinisinr=n2n1 या n1sini=n2sinr
चूँकि कोण i तथा r छोटे है , अतः n1i=n2r ( ∵ sin i=i तथा sinr=r)
n1[ANPO+ANPC]=n2[ANPI+ANPC]
n1PO+n1PC=n2PI+n2PC..(xiii)
नई कार्तीय चिन्ह पध्दति लगने पर , PO=-u, PC=+R , तथा PI=-v
अतः समी (xiii ) से
−n1u+n1R=−n2v+n2R या −n1u+n2v=n2R−n1R
−n1u+n2v=n2−n1R
Topper's Solved these Questions
- BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - भौतिकी (PHYSICS) : 2015EXERCISE - खण्ड - I : (लघु उत्तरीय प्रश्न )11videos
भौतिकी (PHYSICS) : 2015
- BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - भौतिकी (PHYSICS ):2014EXERCISE - खण्ड - घ : दीर्घ उत्तरीय प्रश्न5videos
भौतिकी (PHYSICS ):2014
- BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - भौतिकी 2018EXERCISE - खण्ड अ (दीर्घ उत्तरीय प्रश्न)6videos
भौतिकी 2018
Similar Questions
विद्युत द्विध्रुव-आधूर्ण को परिभाषित करें तथा इसका SI मात्रक लिखे ।
11:23View Solutionसंक्षेप में ट्रांजिस्टर दोलित्र का आधारभूत नियम बताएँ। एक परिपथ चित्र बनाएँ जिसमें प्रेरणिक युग्मन द्वारा पुनर्भरण की प्राप्ति दर्शाई गई हो। दोलित्र अभिक्रिया की व्याख्या करें।
02:18View Solutionकिसी संधारित्र की धारिता को परिभाषित कीजिए। किसी समानान्तर प्लेट संधारित संचित ऊर्जा के लिए व्यंजक स्थापित कीजिए। दिखाएँ कि संधारित्र में संचित ऊर्जा का घनत्व 12ε0E2 होता है, जहाँ E= प्लेटों के बीच का विद्युत-क्षेत्र है।
01:52View SolutionConsider the situation as shown in the figure. If mu_(1) is the friction coefficient between block A and incline and mu_(2) is the friction coefficient between block B and incline. Find the acceleration of block A if (a) mu_(1) = (1)/(5) , mu_(2) =(2)/(5) and (b) mu_(1) = (2)/(5) , mu_(2) = (1)/(5) .
10:55View SolutionThe observer 'O' sees the distance AB as infinitely large. If refractive index of liquid is mu_(1) and that of glass is mu_(2) , then (mu_(1))/(mu_(2)) is : .
04:06View Solution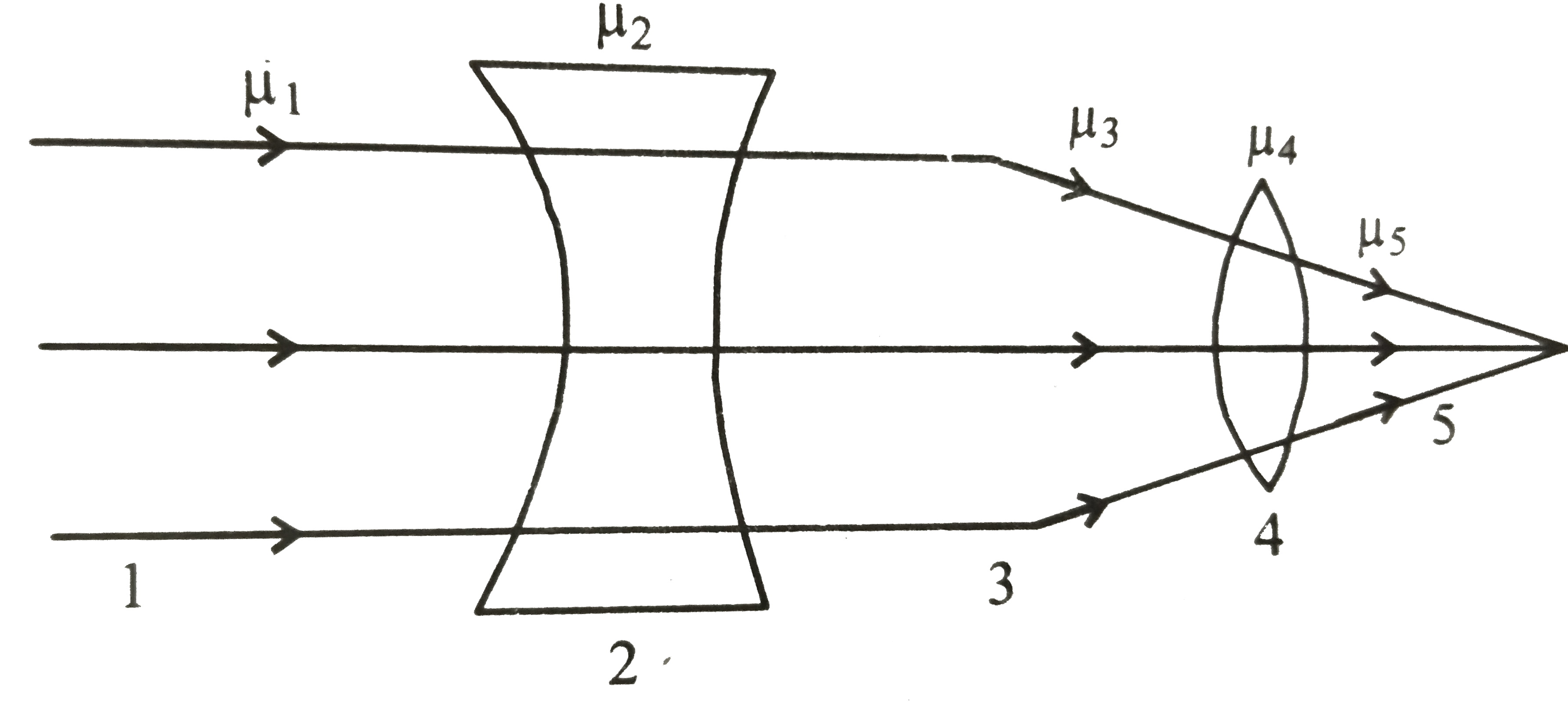
In the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive
indices of the mediums 1,2,3,4 and 5 respectively. Consider
the following:
(1) μ1=μ2 (2) μ3=μ4=μ5
(3) μ2<μ3 (4) μ4>μ5
Which of the above are correct?02:26View Solutionकिसी गोलीय सतह से अपवर्तन के लिए सूत्र μ2v−μ1u=μ2−μ1r निकालें।
01:38View Solutionसदिशों μ1=(1,2,3),μ2=(2,3,1),μ3=(1,3,2) और μ4=(4,6,2) के विषम में निम्नलिखित कथनो पर विचार कीजिये।
I.μ1,μ4 के समान्तर है II. μ2,μ4 के समान्तर है III.μ2,μ3 के समान्तर है
उपरोक्त कथनो में से कोण-सा/से कथन सही है/है?06:01View SolutionThe correct expression for refraction at single convex spherical surface separating two media of refractiv eindices mu_(1) and mu_(2) ( mu_(2) gt mu_(1)) and radius of curvature R is ( u and v are object, image distane respectively )
02:54View SolutionThe reciprocalof ((mu_(2)-mu_(1))/(R)) gives the value of
04:31View Solutionसिद्ध कीजिए कि 1μ2=12μ1.
11:54View SolutionThe refractive indices of a medium for two light waves are μ1andμ2. If μ1>μ2, then which wave will move faster in the medium?
03:51View SolutionThe refractive indices of three media 1,2 and 3 and mu_(1),mu_(2) and mu_(3) respectively (mu_(1) gt mu_(2) gt mu_(3)) . Which of the following statements are correct?
01:38View Solutionसम्बन्ध μ1v−μ2u=μ1−μ2R निकालें जब अवतल गोलीय पृष्ठ से अपेक्षाकृत सघन से अपेक्षाकृत विरल माध्यम (μ2>μ1) में अपवर्तन हो और बनने वाला प्रतिबिम्ब, वास्तविक हो | चिन्ह परिपाटी और अपनाई गई अभिधारणाएँ बताएँ |
06:08View SolutionThe correct expression for refraction at single convex spherical surface separating two media of refractive indices μ1andμ2(μ2>μ1) and radius of curvature R is ( u and v are object, image distane respectively )
02:46View SolutionThe reciprocalof (μ2−μ1R) gives the value of
View Solution
