समीकरण μ=sin[(A+δm)/2]sin(A/2) से μ=1.33 (जल के लिए ) और μ=1.740 (मिथाइल आयोडाइड के लिए) A=60∘ लेते हुए δm निकालें ।
हमें पता हैं कि μ=sin[(A+δm)/2]sin(A/2)
जल के लिए
1.333=sin(60∘+δm2)sin30∘
या sin(60∘+δm2)=1.33×sin30∘
=1.333×0.5000=0.6665
या (60∘+δm2)=41∘48.
या δm=23∘36.
इसी प्रकार हम मिथाइल आयोडाइड के लिए δm=61∘ निकाल सकते हैं।
Topper's Solved these Questions
- समतल पृष्ठों पर अपवर्तनBOOK - GRB PUBLICATION HINDICHAPTER - समतल पृष्ठों पर अपवर्तनEXERCISE - प्रश्नोत्तरी(उच्चस्तरीय चिंतन )
28 Videos
- समतल पृष्ठों पर अपवर्तनBOOK - GRB PUBLICATION HINDICHAPTER - समतल पृष्ठों पर अपवर्तनEXERCISE - प्रश्नोत्तरी 1 अंक
22 Videos
- समतल पृष्ठों पर अपवर्तनBOOK - GRB PUBLICATION HINDICHAPTER - समतल पृष्ठों पर अपवर्तनEXERCISE - विषय -आधारति अभ्यास
35 Videos
- समतल और गोलीय पृष्ठों पर परावर्तन BOOK - GRB PUBLICATION HINDICHAPTER - समतल और गोलीय पृष्ठों पर परावर्तन EXERCISE - अभ्यास
14 Videos
Similar Questions
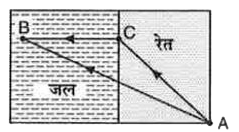
बिंदु B पर चित्र एक तैराक को सहयता चाहिए। बिंदु A पर स्थित दो अलग-अलग जीवनरक्षक(lifeguards) अपने मीनार से एक ही साथ निकलते हैं परन्तु अलग -अलग मार्ग पकड़ते हैं। यद्यपि दोनों जीवनरक्षक रेत पर एक ही चाल से दौड़ते हैं और जल में एक ही चाल से तैरते हैं,फिर भी लम्बा मार्ग (ACB ) पकड़ने वाला जीवनरक्षक,A से B तक छोटा सीधा मार्ग पकड़ने वाले जीवनरक्षक से पहले बिंदु B पर पहले पहुँचता है। व्याख्या करें।
View Solutionएक ही आवृत्ति वाला प्रकाश का स्त्रोत, मछली के टैंक में जल में डुबाया जाता है| बीम, जल में टैंक के पार्श्व पर दोहरे कांच के शीशों में से ( हर काँच के शीशे का μ अलग-अलग है ) और वायु में चलती है। आम तौर पर प्रकाश के (a) आवृत्ति और (b) तरंगदैध्य्र को क्या होता है जब यह बाहर हवा में निकलती है ?
View Solutionकाँच का अपवर्तनांक 1.5 और जल का 1.3 है। यदि जल में प्रकाश की चाल 2.25×108m/s, हो, तो काँच में प्रकाश की चाल क्या है ?
View Solutionकिसी कमरे की दीवार पर लगे समतल दर्पण का न्यूनतम साइज़ निकालें जिससे कमरे के बीचों - बीच खड़ा कोई व्यक्ति अपने पीछे की दीवार का पूरा प्रतिबिम्ब देख सके।
View Solutionसूत्र μ=sin(A+δm2)sin(A2) का निगमन कीजिये| यहाँ μ प्रिज्म के पदार्थ का अपवर्तनांक ,A प्रिज्म का कोण तथा δm अल्पतम विचलन कोण है।
View SolutionA ray of light incident on one face of prism of angle 'A' with refractive index mu .There is no emergent ray if (A) mu>sin((A)/(2)) (B) (B) mu>cos ec((A)/(2)) mu>cos((A)/(2)) (D) mu=sin((A)/(2))
View SolutionA ray of light incident on one face of prism of angle 'A' with refractive index mu .There is no emergent ray if (A) mu>sin((A)/(2)) (B) mu>cos ec((A)/(2)) (C) mu>cos((A)/(2)) (D) mu=sin((A)/(2))
View SolutionAssertion : Refractive index of material of a prism depends on angle of prism A and angle of minimum deviation δm.
Reason : Because μ=sin(A+δm)2sinA/4
View Solutionλ और μ के जिस मान के लिए सदिश a=2ˆi+λˆj−ˆk , सदिश b=3ˆi+ˆj−μˆkके लम्ब है तथा |a|=|b| है , वः मान है
View Solutionकथन : किसी प्रिज्म के पदार्थ का अपवर्तनांक, प्रिज्म कोण A एवं न्यूनतम विचलन कोण δm पर निर्भर करता है
कारण : क्योंकि μ=sin(A+δm2)sin(A/4)
View SolutionFor any prism, prove that .n. or μ=sin(A+δm2)sin(A2) where the terms have their usual meaning
View SolutionFor any prism, prove that .n. or μ=sin(A+δm2)sin(A2) where the terms have their usual meaning
View SolutionFor any prism, prove that .n. or μ=sin(A+δm2)sin(A2) where the terms have their usual meaning
View SolutionDraw a graph to show variation of angle of deviation with that of angle of incidence i for a monochromatic ray of light passing through a glass prism of reflecting angle A. Hence sine deduce the relation μ=sin(A+δm)sinA/2.
Or
What is meant by dispersion of light? Prove that for a prism μ=sin(A+δm)sinA/2, where the symbols have their usual meanings.
Or
Derive the relation, μ=sin(A+δm)sinA/2, when refraction of light takes place through a glass prism. Here every letter has its usual meaning.
View SolutionIf '+' stands for'+', '-' stands for '=', 'x' stands for '+', '+' stands for greater than, '=' stands for less then, '>' stands for multiplication and '<' stands for subtraction, then which of the following alternatives is correct?
View Solution
