Question

For any prism, prove that .n. or $\mu =\frac{\sin \left(\frac{A+{\delta }_m}{2}\right)}{\sin \left(\frac{A}{2}\right)}$ where the terms have their usual meaning

Explanation

In `DeltaQDR`,
`delta=angleDQR+angleDRQ`
`delta=i-r+(i.-r.)`
`=(i+i.)-(r+r.)" "....(1)`

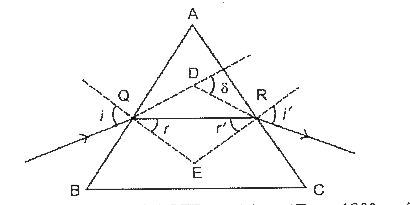
In quadrilateral AQER, `angleA+angleE=180^(@)......(2)`
In `DeltaQER, r+r.+angleE=180^(@)......(3)`
`r+r.=angleA`
[from equations (2) and (3)]
Putting value of rur. in equation (I)
`delta=i+i.-angleA" "...(4)`
In the minimum deviation condition,
`i=i.r=r.,delta-delta_(m),`
So, `r+r.=angleA`
`2r=angleA`
or `r=(angleA)/(2)" ".......(5)`
Equations (4) becomes
`delta_(m)=2i-angleA`
or `i=(angleA+delta_(m))/(2)" "......(6)`
Putting value of i and r from (5) and (6) in Snell.s law,
`n=(sini)/(sinr)`
`n=sin((A+delta_(m))/(2))/((A)/(2)-sin""(A)/(2))`
where, A=Angle of prism
`delta_(m)` =Minimum angle of deviation