A hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
We need to use refraction formula and then mirror formula and then refraction formula again .
Let us first solve for refraction from air to glass .
μ2v−μ1u=μ2−μ1R
⇒ 1.5v−1−2R=1.5−1+R
⇒ 1.5v+12R=12R
⇒v=∞
Hence light ray will become parallel to principal axis after refraction from air to glass .
Silvered part acts like a concave mirror .
Light rays coming parallel to principal axis are converged to focus of concave mirror which is half of the radius of curvature of the surface . we are solving for para-axial rays . Hence after reflection from the concave mirror (formed on the surface of sphere) light ray will converge at a distance R/2 from point B that is pole of the concave mirror formed on polishing the surface of sphere . In the following figure point I is the image formed after reflection from silvered part .
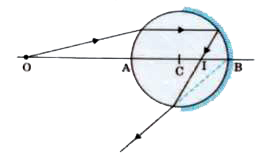
Now point I will act as an object for the refraction from glass to air . Note that after reflection direction of light ray is reversed and so convention of positive and negative will be reversed . Now for the next refraction from glass to air distance will be measured from point A . Distance of point I from point A to R + R /2 = 3R/2 .
Let us apply refraction formula to locate the final image.
μ2v−μ1u=μ2−μ1R
⇒ 1v−1.5−3R/2=1−1.5−R
⇒ 1v+1R=12R
⇒ 1v=12R−1R=−12R
⇒ v=−2R
-2R distance from point A means point B which is pole of the concave mirror . Hence , final image is formed at point B and it is virtual .
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT FILE SOLVED (TEXT BOOK EXERCISES)
Explore 38 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT (EXemplar Problems Obejective Questions) (Multiple Choice Questions (Type-I)
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Conceptual Questions
Explore 40 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
A solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
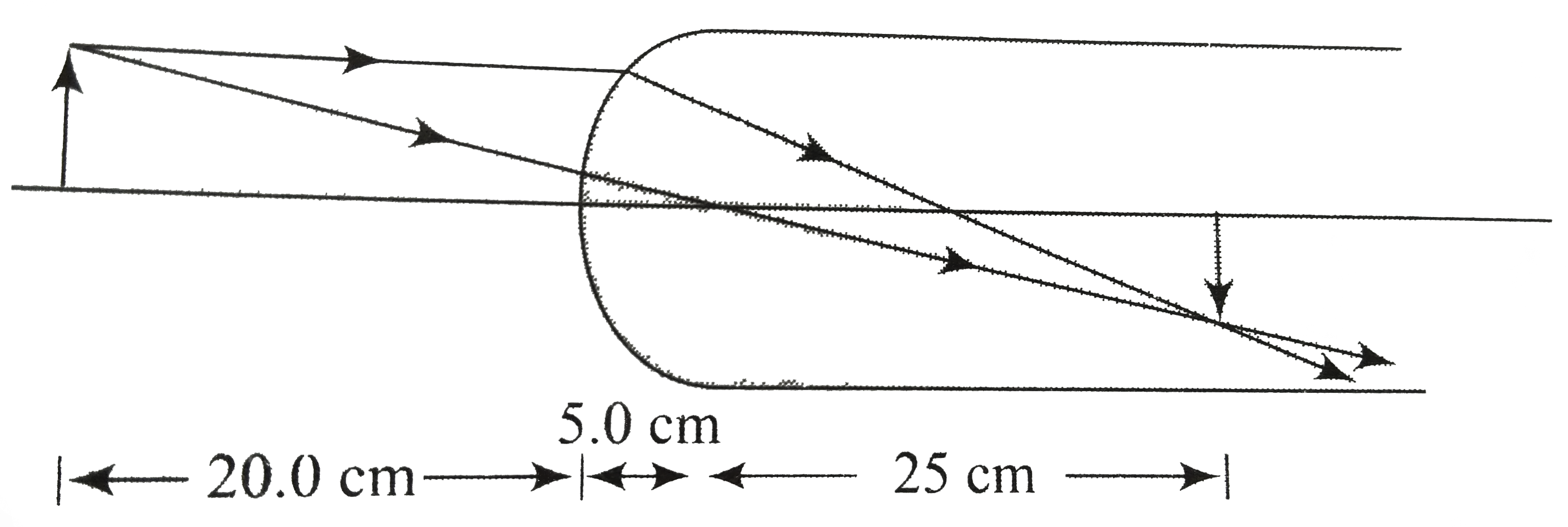
View SolutionOne end of a horizontal cylindrical glass rod (μ=1.5) of radius 0.5cm is rounded in the shape of a hemisphere. An object 0.5mm high is placed perpendicular to the axis of the rod at a distance of 20.0cm from the rounded edge. Locate the image of the object and find its height
View Solution
Knowledge Check
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3An object is placed in front of a sphere of radius R at a distance x from the first surface. The value of x for which the light after refraction from the first surface becomes parallel to the axis is
ARμ−1BRμ+1C2R1+μDRμμ+1There is a small air bubble at the centre of a solid glass sphere of radius 'r' and refractive index μ. What wil be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
ArBrμCr(1−1μ)DZero
A glass sphere (μ=1.5) of radius 8 cm is placed in sunlight. Where is the image of the sun formed by the light passing through the sphere after refraction by second surface of sphere ?
View SolutionOne end of a cylindrical glass rod (mu = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (mu= 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
View SolutionThe radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
View SolutionA mark is made on the surface of a glass sphere of diameter 10 cm and refractive index 1.5. It is viewed through the glass from a portion directly opposite. The distance of the image of the mark from the centre of the sphere will be
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
View Solution

