A glass sphere of diameter 20 cm is constructed with a material of refractive index 1.5. A beam of light strikes the sphere and converges at a point 40 cm behind the pole of a spherical surface. Find the position of the image.
To solve the problem step by step, we will use the lens maker's formula for refraction at a spherical surface.
Step 1: Identify the given values
- Diameter of the glass sphere = 20 cm
- Radius of the sphere (R) = Diameter / 2 = 20 cm / 2 = 10 cm
- Refractive index of glass (μ2) = 1.5
- Refractive index of air (μ1) = 1.0
- The image is formed at a distance (v) = -40 cm (since it is behind the pole)
Step 2: Apply the formula for refraction at a spherical surface
The formula for refraction at a spherical surface is given by:
μ2v−μ1u=μ2−μ1R
Where:
- u is the object distance (which we need to find)
- v is the image distance
- R is the radius of curvature of the sphere
Step 3: Substitute the known values into the formula
Substituting the known values into the formula, we have:
1.5−40−1.0u=1.5−1.010
This simplifies to:
1.5−40−1.0u=0.510
1.5−40−1.0u=0.05
Step 4: Solve for 1.0u
Rearranging the equation gives:
1.0u=1.5−40−0.05
Calculating 1.5−40:
1.5−40=−0.0375
Now substituting this value:
1.0u=−0.0375−0.05
1.0u=−0.0875
Step 5: Calculate u
Taking the reciprocal:
u=1−0.0875≈−11.43 cm
This indicates that the object is located approximately 11.43 cm in front of the pole of the spherical surface.
Step 6: Find the position of the image
Since the image is formed at -40 cm (behind the pole), we can conclude that the image is located at a distance of 40 cm behind the pole of the spherical surface.
Final Answer
The position of the image is 40 cm behind the pole of the spherical surface.
---
- Diameter of the glass sphere = 20 cm
- Radius of the sphere (R) = Diameter / 2 = 20 cm / 2 = 10 cm
- Refractive index of glass (μ2) = 1.5
- Refractive index of air (μ1) = 1.0
- The image is formed at a distance (v) = -40 cm (since it is behind the pole)
The formula for refraction at a spherical surface is given by:
μ2v−μ1u=μ2−μ1R
Where:
- u is the object distance (which we need to find)
- v is the image distance
- R is the radius of curvature of the sphere
Substituting the known values into the formula, we have:
1.5−40−1.0u=1.5−1.010
This simplifies to:
1.5−40−1.0u=0.510
1.5−40−1.0u=0.05
Rearranging the equation gives:
1.0u=1.5−40−0.05
Calculating 1.5−40:
1.5−40=−0.0375
Now substituting this value:
1.0u=−0.0375−0.05
1.0u=−0.0875
Taking the reciprocal:
u=1−0.0875≈−11.43 cm
This indicates that the object is located approximately 11.43 cm in front of the pole of the spherical surface.
Since the image is formed at -40 cm (behind the pole), we can conclude that the image is located at a distance of 40 cm behind the pole of the spherical surface.
The position of the image is 40 cm behind the pole of the spherical surface.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (1)
Explore 13 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (2)
Explore 9 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
A beam of light strikes a glass sphere of diameter 15cm convering towards a point 30cm behind the pole of the spherical surface. Find the position of the image, if μ of glass is 1.5.
View SolutionA sunshine recorder globe is a device that provides the information about climate and weather by recording the amount of sunshine for a given location. One such globe of diameter 20 cm and refractive index 1.5 is used for the purpose. A parallel beam of light enters the globe and is refracted by the spherical surface of the globe. Determine the position of the image of the rays formed.
View Solution
Knowledge Check
A clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
A−3RB+3RC−RD+R
A double convex spherical glass has refractive index 1.5 and both radius of curvature 30 cm. A point object is placed at a distance of 120 cm from the spherical glass. What will be the position of the image formed ?
View SolutionThere is a spherical glass shell of refractive index 1.5, inner radius 10 cm and outer radius 20 cm. Inside th espherical cavity, there is air. A point object is placed at a point O at a distance of 30cm from the outer spherical surface. Find the final position of th eimage as seen eye.
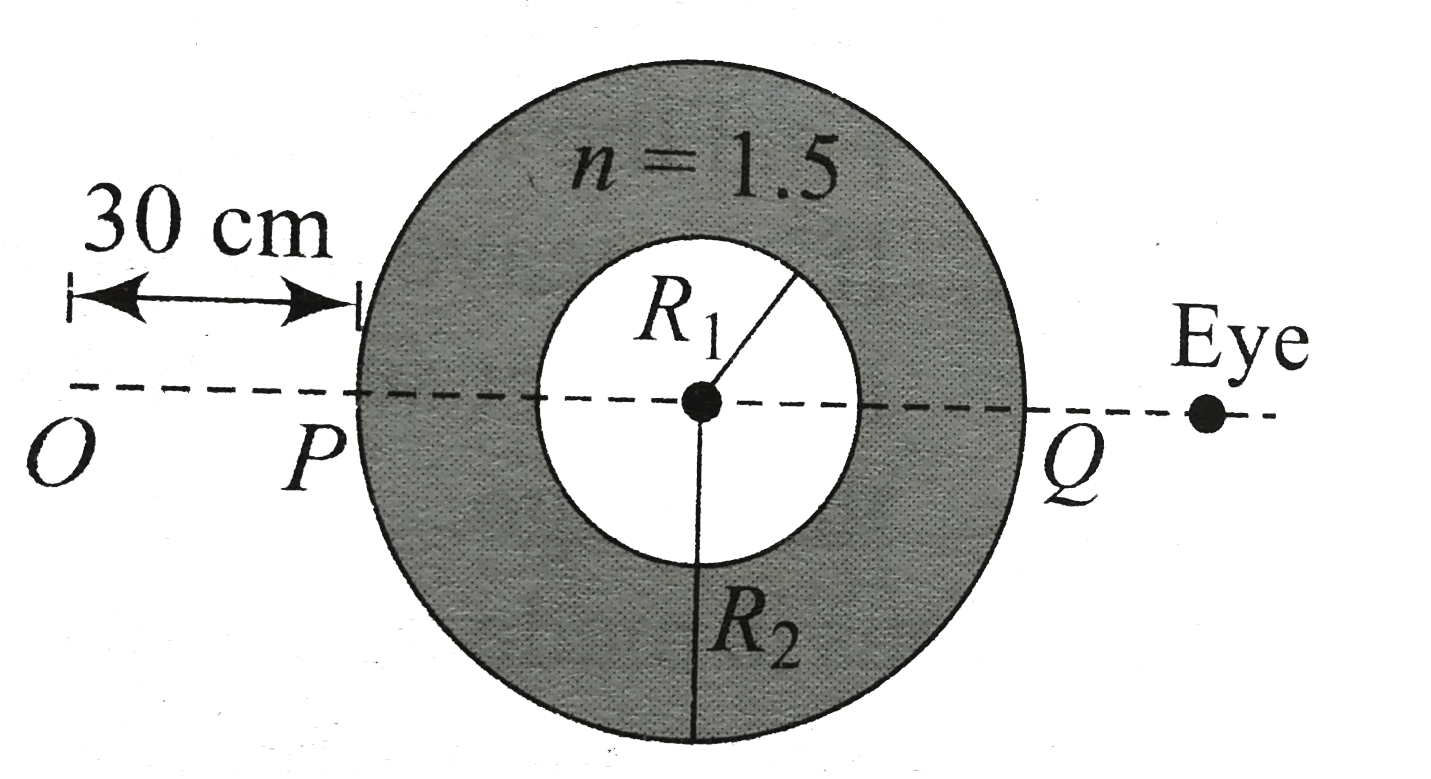
View SolutionA hollow sphere made of a transparent material of refractive index 1.5 has a small mark on its surface as shown. The mark is observed from the farther side. Find the distance of the image of mark from the centre of the sphere.

View SolutionA glass sphere (μ=1.5) of radius 8 cm is placed in sunlight. Where is the image of the sun formed by the light passing through the sphere after refraction by second surface of sphere ?
View SolutionA biconvex lens has radii of curvature 20 cm and 40cm. The refractive index of the material of the lens is 1.5. An object is placed 40cm in front of the lens. Calculate the psition of the image.
View SolutionThere is a glass sphere of radius 20 cm having refractive index 1.5. A point object is embedded inside it at a distance 6 cm to the left of the centre. Locate the image for observer looking from left. Locate the image for observer looking from right.
View SolutionA small LED, emitting light is placed at x distance above a spherical glass of refractive index 1.5 and radius of curvature 30 cm. The image of the LED is formed at a distance of 150 cm away from the surface of sphere along the direction of incident light. Calculate the distance between LED light and the surface of spherical glass.
View Solution

