A biconvex lens has radii of curvature 20 cm and 40cm. The refractive index of the material of the lens is 1.5. An object is placed 40cm in front of the lens. Calculate the psition of the image.
To solve the problem step by step, we will use the lens maker's formula and the lens formula to find the position of the image formed by the biconvex lens.
Step 1: Determine the focal length of the lens using the lens maker's formula.
The lens maker's formula is given by:
1f=(μ−1)(1R1−1R2)
Where:
- μ is the refractive index of the lens material.
- R1 is the radius of curvature of the first surface (positive for biconvex).
- R2 is the radius of curvature of the second surface (negative for biconvex).
Given:
- R1=20cm
- R2=−40cm (since it is the second surface)
- μ=1.5
Substituting these values into the formula:
1f=(1.5−1)(120−1−40)
Calculating:
1f=0.5(120+140)
Finding a common denominator (which is 40):
1f=0.5(240+140)=0.5(340)=380
Thus, the focal length f is:
f=803cm≈26.67cm
Step 2: Use the lens formula to find the image position.
The lens formula is given by:
1f=1v−1u
Where:
- v is the image distance.
- u is the object distance (negative for real objects).
Given that the object is placed 40 cm in front of the lens:
u=−40cm
Substituting the values into the lens formula:
1803=1v−1−40
This simplifies to:
380=1v+140
Finding a common denominator (which is 80):
380=280+1v
Rearranging gives:
1v=380−280=180
Thus, we find:
v=80cm
Conclusion
The position of the image is at v=80cm on the opposite side of the lens.
---
- μ is the refractive index of the lens material.
- R1 is the radius of curvature of the first surface (positive for biconvex).
- R2 is the radius of curvature of the second surface (negative for biconvex).
- R1=20cm
- R2=−40cm (since it is the second surface)
- μ=1.5
- v is the image distance.
- u is the object distance (negative for real objects).
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.7
21 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.5
22 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A bicovex lens has radii of cuvature 20 cm each. If the refractive index of the material of the lens is 1.5, what is its focal length?
View SolutionA plano-convex lens is silvered on its plane side. The radius of curvature of the other face is 12cm and the refractive index of the material of the lens is 1.5. An object is placed 24 cm in front of the silvered lens. Where will the image be formed?
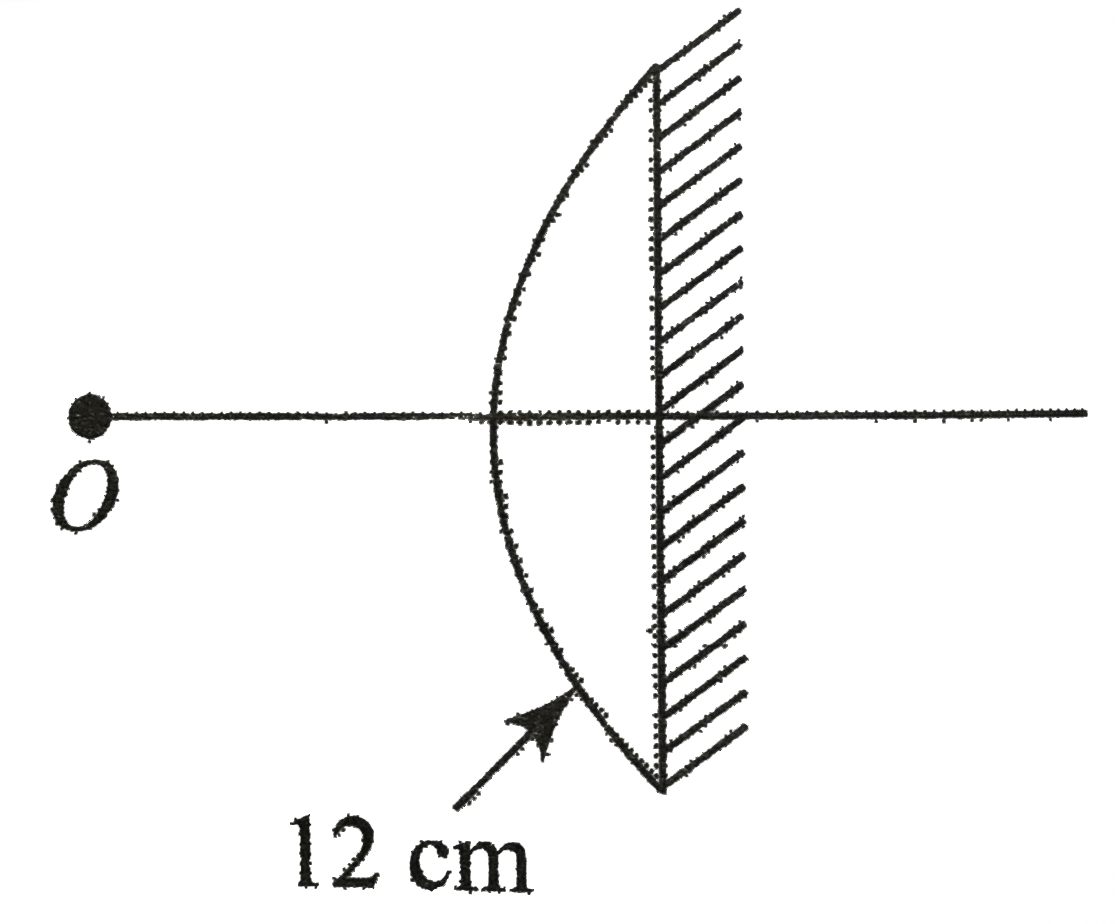
View Solution
Knowledge Check
A concave lens has radioi of curvatures of 20 cm and 30 cm respectively. If the refrative index of the material of lens is 1.6 it focal length is given by
A−30 cmB−25cmC−20cmD−10cmA double convex lens has faces of radii of curvature 30 cm each. The refractive index of the material of the lens is 1.5. What is the focal length of this lens when immersed is carbondisulphide of refractive index 1.6 ?
A−120cmB−180cmC−200cmD−240cmPower of biconvex lens is 10 diopters and radius of curvature of each surface is 10cm.Then refractive index of material of lens is
A43924B44082C43954D43892
A converging bundle of rays is intercepted by a biconcave lens. The radii of curvature of both surfaces are 20cm and the refractive index of the material of the lens is 1.5. If the rays originially converged to a point 10cm in front of the lens, where will they now converge after passing through the lens?

View SolutionThere is a glass (μ=1.5) biconvex lens of radius of curvature 5 cm and thickness of the lens is also 5 cm. An object is placed at a distance 20 cm from the front surface of lens. Locate its final image.
View SolutionA glass slab of thickness 2cm and refractive index 2 is placed in contact with a biconvex lens of focal length 20cm. The refractive index of the material of the lens 1.5 . The far side of the lens is silvered. Where should an object be placed in front of the slab so that it images on to itself?
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe power of a biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
View Solution
