Assertion : Object A of mass collides elastically with another object B of same mass at rest and if found that A and B move perpendicular to each other after collision .
Reason : Collision between A and B is not head on .
If both assertion and reason are corret and reason is a correct explanation of the assertion .
If both assertion and reason are correct but reason is ot the correct explanation of assertion .
If assertion is correct but reason is incorrect .
If both assertion and reason are incorrect .
The correct Answer is:A
To solve the problem, we need to analyze the assertion and the reason provided.
Step 1: Understanding the Assertion
The assertion states that object A of mass collides elastically with another object B of the same mass at rest, and after the collision, A and B move perpendicular to each other.
Step 2: Understanding Elastic Collision
In an elastic collision, both momentum and kinetic energy are conserved. If two objects of the same mass collide elastically, the velocities after the collision can be determined based on their initial velocities.
Step 3: Analyzing the Collision
1. Initial Conditions:
- Let the mass of object A be m and its initial velocity be u1.
- Let the mass of object B be m (at rest), so its initial velocity u2=0.
2. Final Velocities:
- After the collision, let the velocity of A be vA and the velocity of B be vB.
- According to the problem, vA and vB are perpendicular to each other.
Step 4: Conservation of Momentum
The conservation of momentum before and after the collision can be expressed as:
mu1+mu2=mvA+mvB
Since u2=0, this simplifies to:
mu1=mvA+mvB
Dividing through by m gives:
u1=vA+vB
Step 5: Conservation of Kinetic Energy
The conservation of kinetic energy in an elastic collision can be expressed as:
12mu21=12mv2A+12mv2B
Again, dividing through by 12m gives:
u21=v2A+v2B
Step 6: Relationship Between Velocities
Since vA and vB are perpendicular, we can use the Pythagorean theorem:
v2A+v2B=u21
This confirms that the velocities can satisfy both the momentum and kinetic energy conservation equations.
Step 7: Conclusion
Since A and B move perpendicular to each other after the collision, it indicates that the collision is not head-on. In a head-on elastic collision, the velocities would simply exchange if the masses are equal, which does not happen here.
Final Answer
- Assertion: True
- Reason: True
- The reason correctly explains the assertion.
The assertion states that object A of mass collides elastically with another object B of the same mass at rest, and after the collision, A and B move perpendicular to each other.
In an elastic collision, both momentum and kinetic energy are conserved. If two objects of the same mass collide elastically, the velocities after the collision can be determined based on their initial velocities.
1. Initial Conditions:
- Let the mass of object A be m and its initial velocity be u1.
- Let the mass of object B be m (at rest), so its initial velocity u2=0.
- After the collision, let the velocity of A be vA and the velocity of B be vB.
- According to the problem, vA and vB are perpendicular to each other.
The conservation of momentum before and after the collision can be expressed as:
mu1+mu2=mvA+mvB
Since u2=0, this simplifies to:
mu1=mvA+mvB
Dividing through by m gives:
u1=vA+vB
The conservation of kinetic energy in an elastic collision can be expressed as:
12mu21=12mv2A+12mv2B
Again, dividing through by 12m gives:
u21=v2A+v2B
Since vA and vB are perpendicular, we can use the Pythagorean theorem:
v2A+v2B=u21
This confirms that the velocities can satisfy both the momentum and kinetic energy conservation equations.
Since A and B move perpendicular to each other after the collision, it indicates that the collision is not head-on. In a head-on elastic collision, the velocities would simply exchange if the masses are equal, which does not happen here.
- Assertion: True
- Reason: True
- The reason correctly explains the assertion.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Matrix Match Type Questions)
Explore 2 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Integer Type Questions)
Explore 7 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (D. Multiple Choice Questions)
Explore 10 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
An object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View SolutionA body of a mass m moving with speed v collides elastically head on with another body of mass m, initially at rest. Show that the moving body will come to a stop after collision.
View Solution
Knowledge Check
An object of mass M1 moving horizontally with speed u collides elastically with another object of mass M2 at rest. Select correct statement.
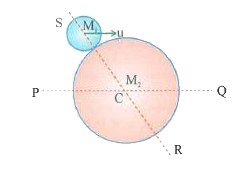 AThe momentum of system is conserved only in direction PQBMomentum of M1 is conserved in direction perpendicular to SRCMomentum of M2 will change in direction normal to CRDAll of these
AThe momentum of system is conserved only in direction PQBMomentum of M1 is conserved in direction perpendicular to SRCMomentum of M2 will change in direction normal to CRDAll of theseA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
Aboth the balls come to restBthe velocities are exchanged between the two ballsCboth of them move at right angles to the original line of motionDone ball comes to rest and another ball travels back with velocity 2vBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
A59B19C89D49
Prove that in a two dimensional elastic collision of a moving ball with another stationary identical ball, the two balls move perpendicular to each other after collision?
View SolutionA body of mass m makes an elastic collision with another identical body at rest. Show that if the collisionis not head on the bodiese to at right to each other after the collision.
View SolutionA ball of mass m makes an elastic collision with another identical ball at rest. Show that if the collision is oblique, the bodies go at right angles to each other after collision.
View SolutionA body A collides elastically with another body B at rest . The bodies A and B move in opposite directions with same speeds . Calculate the ratio of masses of A and B .
View SolutionIf one sphere collides head - on with another sphere of the same mass at rest inelastically. The ratio of their speeds (v2v1) after collision shall be
View Solution

