Consider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
If a speed given at top is √gR3 , then what is the angle made by radius through block when it leaves the sphere ?
cos−1(23)
cos−1(34)
cos−1(59)
cos−1(79)
The correct Answer is:D
First we can apply conservation of mechanical energy between top point and the point where radius through the aprticle makes an angle θ with the vertical .
Gain in K.E = Loss of gravitational potential energy
⇒ 12mv22−12mv21=mgR(1−cosθ)
Substituting v1=√gR3 we get the following :
⇒12mv22−12mgR3=mgR(1−cosθ)
⇒12mv22−mgR6=mgR(1−cosθ)
⇒ 12mv22=mgR(76−cosθ)
⇒ mv22R=2mg(76−cosθ) ...(ii)
According to circular dynamics we can write the following :
mgcosθ−N2=mv22R
Substituting from equation (ii) and N2=0, we get
mgcosθ=2mg(76−cosθ)⇒cosθ=2(76−cosθ)
⇒ cosθ=73−2coθ⇒3cosθ=73⇒cosθ=79
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Assertion Reason Type Questions)
Explore 13 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Matrix Match Type Questions)
Explore 2 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (C. Multiple Choice Questions)
Explore 16 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View SolutionA smooth hemisphere is kept fixed on a horizontal floor . A small block f mass m is kept on the tip of hemisphere . Block is slightly pushed and it is found that block leaves contact with the spherical surface when radius through the block makes and angle θ with the vartical . Calculate θ .
View Solution
Knowledge Check
Consider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
What is the normal reaction between block and the sphere just after the impulse is applied ?Amv2RBmg−mv2RCmgD0Consider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
What si the maximum possible value of v so that block does not lose contact with the sphere at the top point ?A√5gRB√3gRC√gRD0A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gR
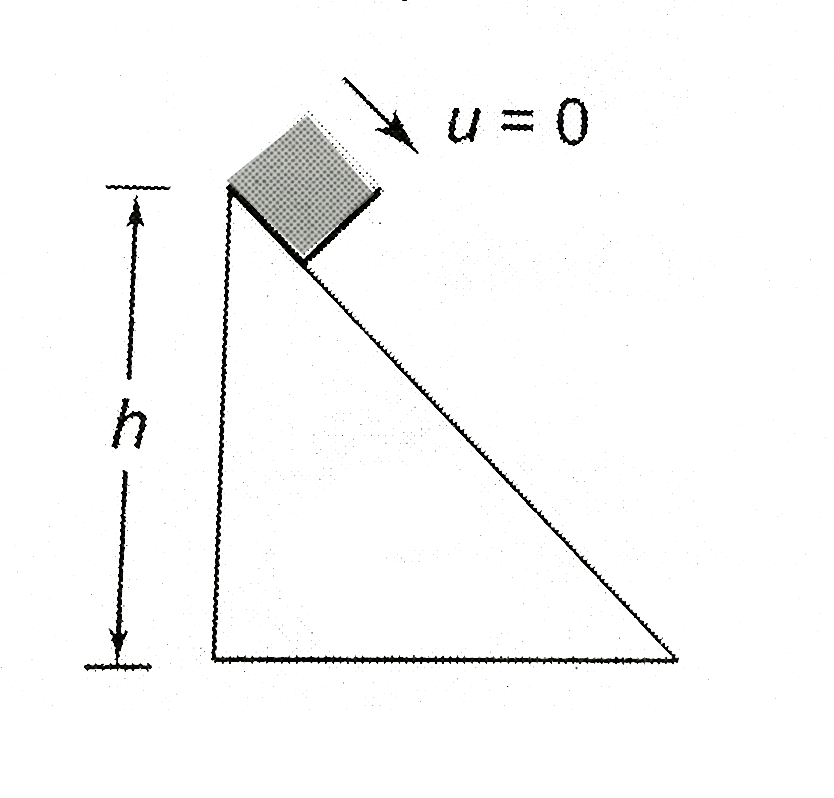
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA particle of mass m is kept on the top of a smooth sphere of radius LR. It is given a sharp impulse whichimparts it a horizontal speed v. a. find thenormal force between the sphere and the particle just after the impulse. B. What should be the minimum value of v for which the particle does not slip on the sphere? c. Assuming the velocity v to be half the minimum calculated in part, d. find teh angle made by the radius through the particle with the vertical when it leaves the sphere.

View SolutionA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
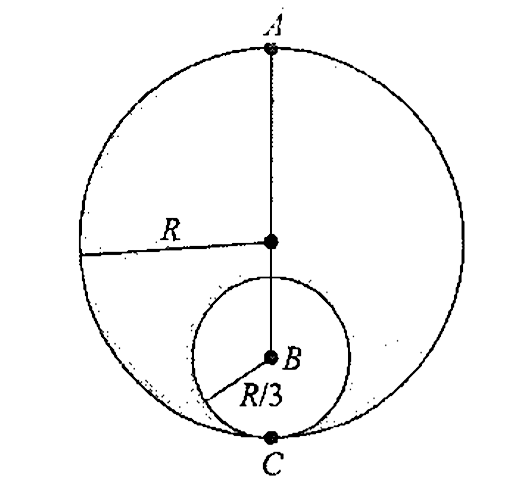
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
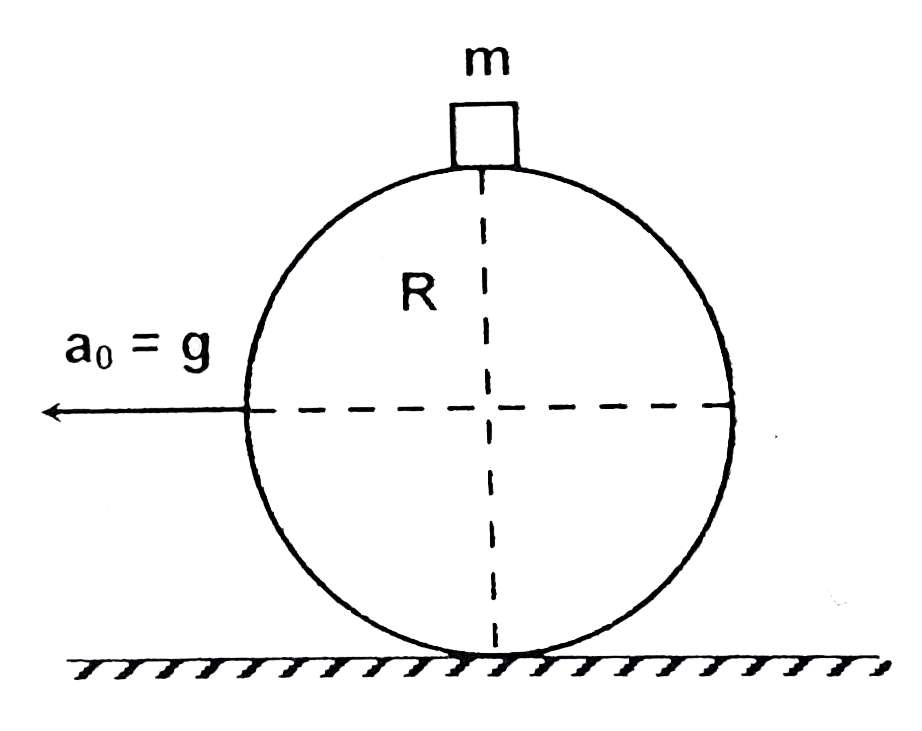
View SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
View Solution

