Consider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
What is the normal reaction between block and the sphere just after the impulse is applied ?
mv2R
mg−mv2R
mg
0
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the block just after the impulse is applied. Here's a step-by-step solution:
Step 1: Identify the forces acting on the block
When the block is at the topmost point of the sphere, two main forces act on it:
1. The weight of the block, W=mg, acting downwards.
2. The normal reaction force N exerted by the sphere on the block, acting perpendicular to the surface of the sphere (also downwards at this point).
Step 2: Understand the motion of the block
After the impulse is applied, the block starts moving with a speed v horizontally. As it moves, it will also experience a centripetal acceleration because it is moving in a circular path around the center of the sphere.
Step 3: Apply the centripetal force concept
For the block to maintain circular motion at the topmost point, the net force acting towards the center of the sphere must provide the necessary centripetal force. The centripetal force Fc required for the block moving with speed v at radius R is given by:
Fc=mv2R
Step 4: Set up the equation for forces
At the topmost point, the net force towards the center of the sphere is the difference between the weight of the block and the normal reaction force:
Fc=mg−N
Substituting the expression for centripetal force:
mv2R=mg−N
Step 5: Solve for the normal reaction force N
Rearranging the equation gives us:
N=mg−mv2R
Conclusion
Thus, the normal reaction between the block and the sphere just after the impulse is applied is:
N=mg−mv2R
When the block is at the topmost point of the sphere, two main forces act on it:
1. The weight of the block, W=mg, acting downwards.
2. The normal reaction force N exerted by the sphere on the block, acting perpendicular to the surface of the sphere (also downwards at this point).
After the impulse is applied, the block starts moving with a speed v horizontally. As it moves, it will also experience a centripetal acceleration because it is moving in a circular path around the center of the sphere.
For the block to maintain circular motion at the topmost point, the net force acting towards the center of the sphere must provide the necessary centripetal force. The centripetal force Fc required for the block moving with speed v at radius R is given by:
Fc=mv2R
At the topmost point, the net force towards the center of the sphere is the difference between the weight of the block and the normal reaction force:
Fc=mg−N
Substituting the expression for centripetal force:
mv2R=mg−N
Rearranging the equation gives us:
N=mg−mv2R
Thus, the normal reaction between the block and the sphere just after the impulse is applied is:
N=mg−mv2R
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Assertion Reason Type Questions)
Explore 13 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Matrix Match Type Questions)
Explore 2 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (C. Multiple Choice Questions)
Explore 16 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
The system described in previous question is kept on a frictionless horizontal floor with spring at its natural length. Now a sharp impulse is applied on the block m2 to impart it a speed of v. Calculate velocity acquired by the centre of mass just after the impulse is applied on the block m2. Also calculate maximum possible elongation suffered by the spring.

View SolutionAOB is a smooth semicircular track of radius r. A block of mass m is given a velocity √2rg parallel to track at point A. Calculate normal reaction between block and track when block reaches at point O.

View Solution
Knowledge Check
Consider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
What si the maximum possible value of v so that block does not lose contact with the sphere at the top point ?A√5gRB√3gRC√gRD0Consider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
If a speed given at top is √gR3 , then what is the angle made by radius through block when it leaves the sphere ?Acos−1(23)Bcos−1(34)Ccos−1(59)Dcos−1(79)Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.
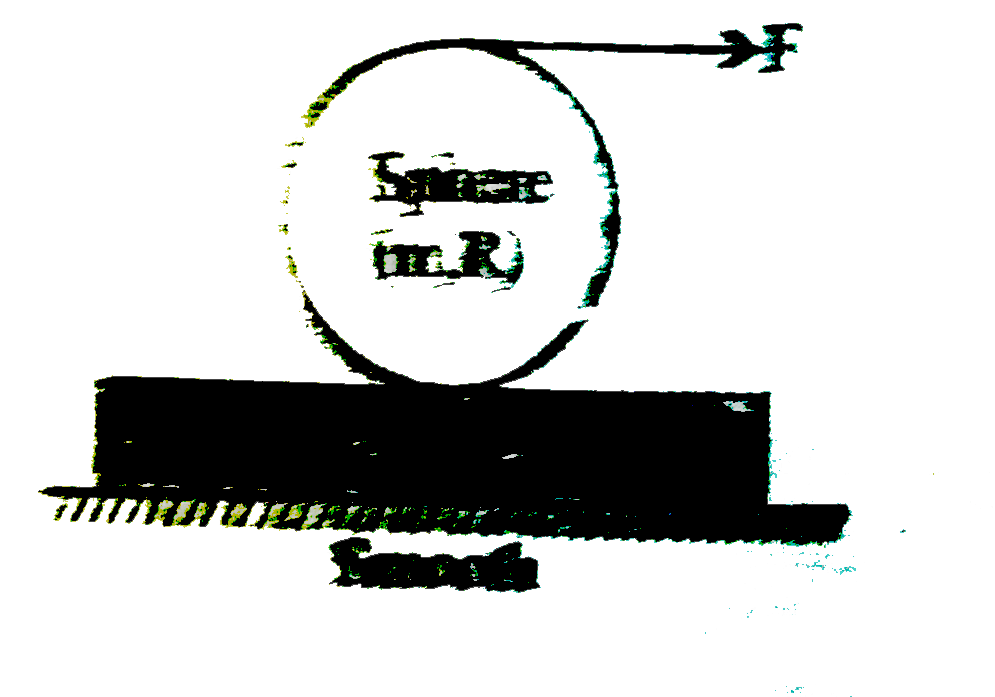
Acceleration of the plank isA3F16mB11F8mC9F4mDZero
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA particle of mass m is kept on the top of a smooth sphere of radius LR. It is given a sharp impulse whichimparts it a horizontal speed v. a. find thenormal force between the sphere and the particle just after the impulse. B. What should be the minimum value of v for which the particle does not slip on the sphere? c. Assuming the velocity v to be half the minimum calculated in part, d. find teh angle made by the radius through the particle with the vertical when it leaves the sphere.

View SolutionConsider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Friction force acting between the sphere and the plank is
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

View SolutionA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
View Solution

