Two blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion
Accelerations of both the objects are equal and opposite of each other .
Velocities of both the bjects are equal and opposite of each other .
Forces acting on both the objects are equal and opposite of each other
Linear momenta of both the objects are equal and opposite of each other .
The correct Answer is:C, D
To solve the problem, let's analyze the situation step by step:
Step 1: Understand the System
We have two blocks connected by a spring. When the blocks are pulled apart and released, they will experience forces due to the spring trying to return to its natural length.
Step 2: Identify Forces Acting on the Blocks
When the spring is extended, it exerts a force on both blocks. The force exerted by the spring on each block is given by Hooke's Law:
F=−kx
where k is the spring constant and x is the displacement from the natural length of the spring.
Step 3: Analyze the Acceleration
Let’s denote the masses of the blocks as m1 and m2. The acceleration of each block can be calculated using Newton's second law:
a1=Fspringm1anda2=Fspringm2
Since the forces acting on both blocks are equal in magnitude but opposite in direction, the accelerations a1 and a2 will not necessarily be equal unless the masses are the same.
Step 4: Analyze the Velocities
Since there are no external forces acting on the system, the total momentum of the system is conserved. Initially, the system is at rest, so the total momentum is zero:
0=m1v1+m2v2
This implies:
m1v1=−m2v2
This means that the velocities v1 and v2 are not equal but are opposite in direction.
Step 5: Analyze the Forces
As discussed, the forces acting on both blocks are equal in magnitude and opposite in direction:
F1=kxandF2=−kx
Thus, the forces are equal and opposite, confirming that option C is correct.
Step 6: Analyze the Linear Momentum
From the conservation of momentum, we have already established that:
m1v1+m2v2=0
This indicates that the linear momentum of the two blocks is equal in magnitude and opposite in direction, confirming that option D is also correct.
Conclusion
The correct answers to the options provided in the question are:
- C: Forces acting on both objects are equal and opposite to each other.
- D: Linear momentum of both objects are equal and opposite to each other.
---
We have two blocks connected by a spring. When the blocks are pulled apart and released, they will experience forces due to the spring trying to return to its natural length.
When the spring is extended, it exerts a force on both blocks. The force exerted by the spring on each block is given by Hooke's Law:
F=−kx
where k is the spring constant and x is the displacement from the natural length of the spring.
Let’s denote the masses of the blocks as m1 and m2. The acceleration of each block can be calculated using Newton's second law:
a1=Fspringm1anda2=Fspringm2
Since the forces acting on both blocks are equal in magnitude but opposite in direction, the accelerations a1 and a2 will not necessarily be equal unless the masses are the same.
Since there are no external forces acting on the system, the total momentum of the system is conserved. Initially, the system is at rest, so the total momentum is zero:
0=m1v1+m2v2
This implies:
m1v1=−m2v2
This means that the velocities v1 and v2 are not equal but are opposite in direction.
As discussed, the forces acting on both blocks are equal in magnitude and opposite in direction:
F1=kxandF2=−kx
Thus, the forces are equal and opposite, confirming that option C is correct.
From the conservation of momentum, we have already established that:
m1v1+m2v2=0
This indicates that the linear momentum of the two blocks is equal in magnitude and opposite in direction, confirming that option D is also correct.
The correct answers to the options provided in the question are:
- C: Forces acting on both objects are equal and opposite to each other.
- D: Linear momentum of both objects are equal and opposite to each other.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (D. Multiple Choice Questions)
Explore 10 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Assertion Reason Type Questions)
Explore 13 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (JEE (Advanced) for IIT Entrance)
Explore 7 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
Two blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -

View Solution
Knowledge Check
Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
A12kx2B−12kx2C14kx2D−14kx2Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
A12kx2B−12kx2C14kx2D−14kx2Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
A12kx2B−12kx2C14kx2D−14kx2
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
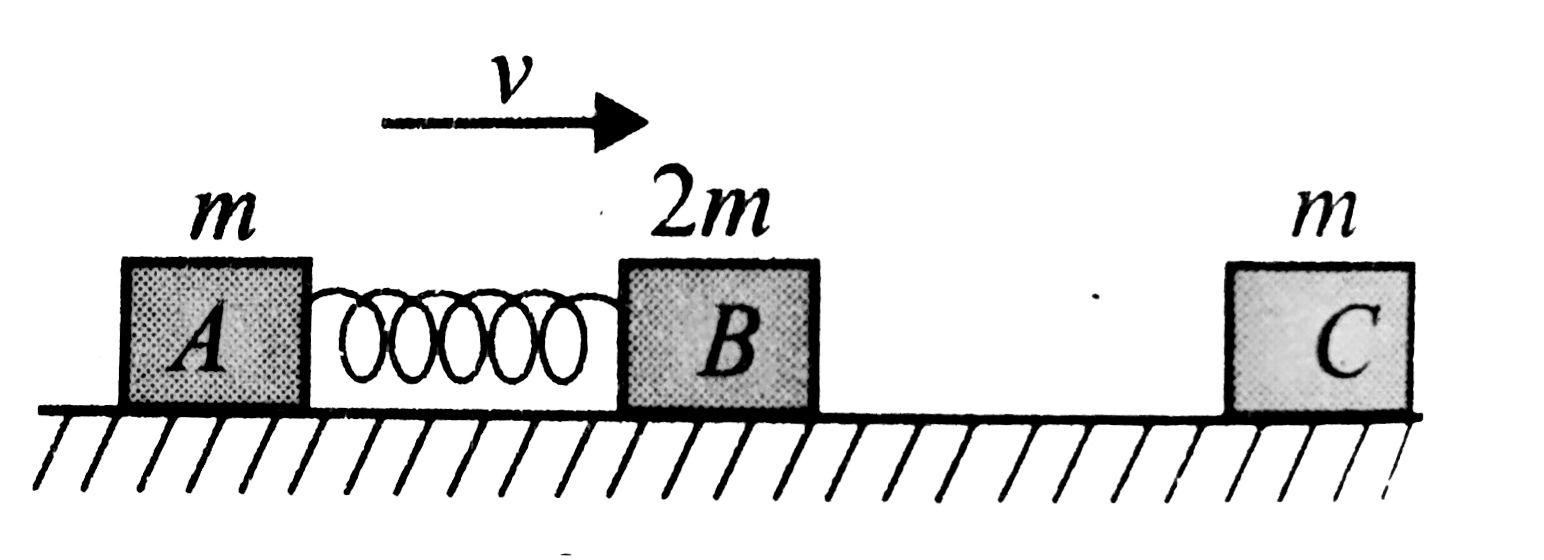
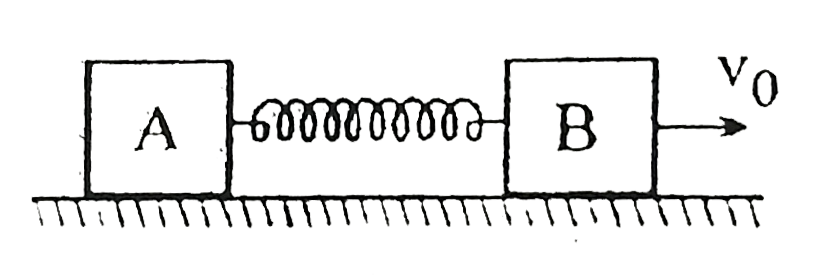
View SolutionTwo blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionConsider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
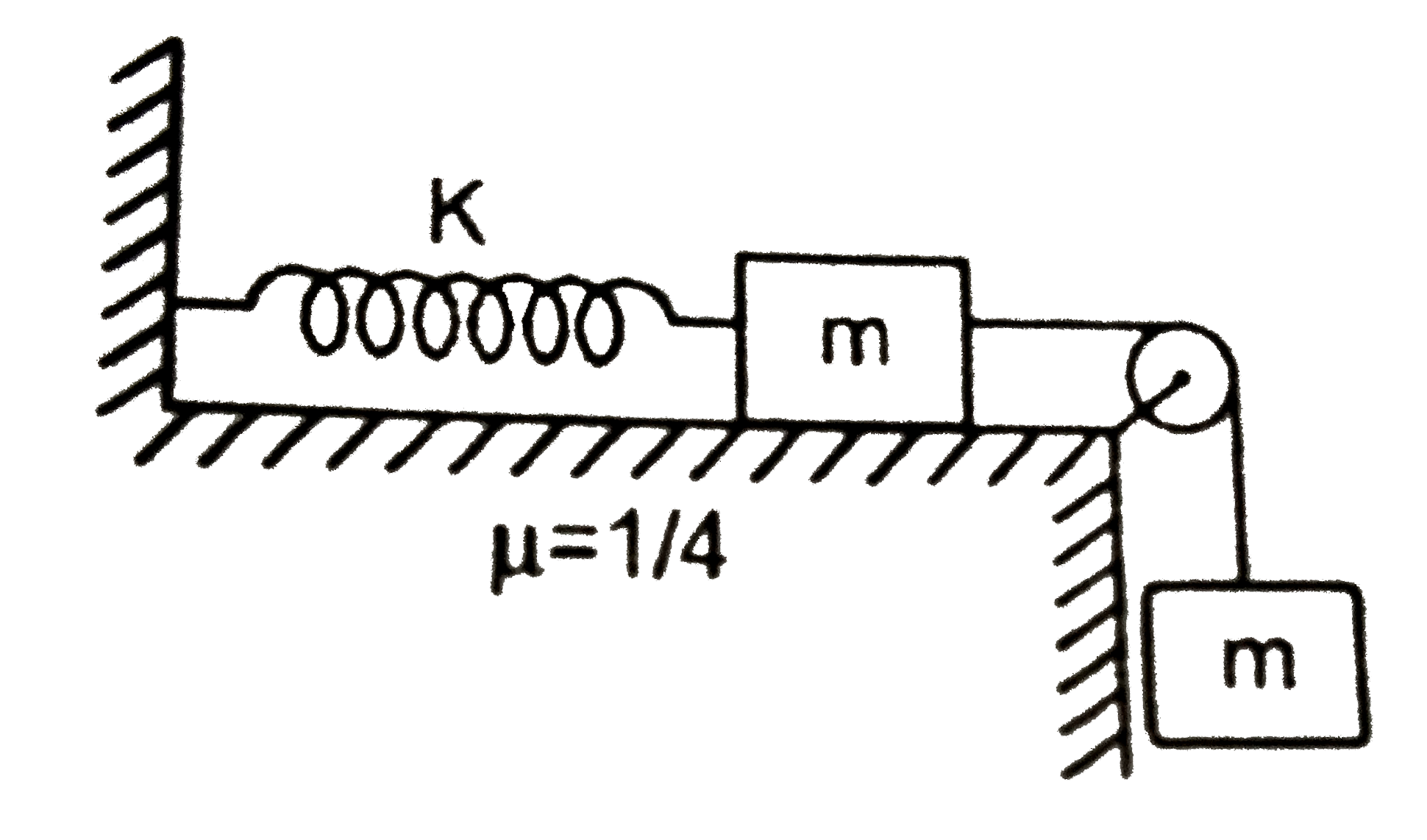
If the string connecting both the masses is cut just at the instant both masses came to momentary rest for the first time in question 5, then maximum compression of spring during resulting motion is (Take μ=1/4)
View Solution

