When two bodies of equal masses collide elastically then
Linear momenta are exchanged
Velocities are exchanged
Speeds are exchanged
Slower body speeds up for and faster body slows down .
The correct Answer is:A, B, C, D
To solve the problem of what happens when two bodies of equal masses collide elastically, we can break it down step by step.
1. Understanding Elastic Collision:
- In an elastic collision, both momentum and kinetic energy are conserved. This means that the total momentum and total kinetic energy before the collision will be equal to the total momentum and total kinetic energy after the collision.
2. Define the Masses and Initial Velocities:
- Let the mass of each body be m.
- Let the initial velocities of the two bodies be u1 and u2, where u1 is the velocity of the first body and u2 is the velocity of the second body.
3. Collision Scenario:
- Assume the first body is moving towards the second body. After the collision, the velocities of the two bodies will change.
4. Final Velocities After Collision:
- For two bodies of equal mass colliding elastically, the final velocities are exchanged. This means:
- The first body will have a final velocity of u2.
- The second body will have a final velocity of u1.
5. Analysis of the Outcomes:
- Direction and Magnitude: The direction of the velocities remains the same, but the magnitudes are exchanged.
- Speeds Interchanged: The speeds of the two bodies are interchanged after the collision.
- Linear Momentum Exchange: The linear momentum of the bodies before and after the collision is also exchanged. Initially, the momentum of the first body is m⋅u1 and for the second body is m⋅u2. After the collision, the first body has momentum m⋅u2 and the second body has momentum m⋅u1.
- Speed Changes: The slower body speeds up while the faster body slows down. For example, if one body was moving at 4 m/s and the other at 3 m/s, after the collision, the body that was moving at 3 m/s will now move at 4 m/s and vice versa.
Conclusion:
All the statements regarding the outcomes of the elastic collision between two bodies of equal mass are correct:
- The direction and magnitude of velocities are maintained.
- Speeds are interchanged.
- Linear momenta are exchanged.
- The slower body speeds up and the faster body slows down.
- In an elastic collision, both momentum and kinetic energy are conserved. This means that the total momentum and total kinetic energy before the collision will be equal to the total momentum and total kinetic energy after the collision.
- Let the mass of each body be m.
- Let the initial velocities of the two bodies be u1 and u2, where u1 is the velocity of the first body and u2 is the velocity of the second body.
- Assume the first body is moving towards the second body. After the collision, the velocities of the two bodies will change.
- For two bodies of equal mass colliding elastically, the final velocities are exchanged. This means:
- The first body will have a final velocity of u2.
- The second body will have a final velocity of u1.
- Direction and Magnitude: The direction of the velocities remains the same, but the magnitudes are exchanged.
- Speeds Interchanged: The speeds of the two bodies are interchanged after the collision.
- Linear Momentum Exchange: The linear momentum of the bodies before and after the collision is also exchanged. Initially, the momentum of the first body is m⋅u1 and for the second body is m⋅u2. After the collision, the first body has momentum m⋅u2 and the second body has momentum m⋅u1.
- Speed Changes: The slower body speeds up while the faster body slows down. For example, if one body was moving at 4 m/s and the other at 3 m/s, after the collision, the body that was moving at 3 m/s will now move at 4 m/s and vice versa.
All the statements regarding the outcomes of the elastic collision between two bodies of equal mass are correct:
- The direction and magnitude of velocities are maintained.
- Speeds are interchanged.
- Linear momenta are exchanged.
- The slower body speeds up and the faster body slows down.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (D. Multiple Choice Questions)
Explore 10 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Assertion Reason Type Questions)
Explore 13 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (JEE (Advanced) for IIT Entrance)
Explore 7 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A body of a mass m moving with speed v collides elastically head on with another body of mass m, initially at rest. Show that the moving body will come to a stop after collision.
View SolutionTwo Particle of equal masses 4M are initially at rest. A particle of mass M moving at speed u collide elastically with one of the larger balls. How many collision occure?

View Solution
Knowledge Check
When two bodies collide elastically, then
AKinetic energy of the system alone is conservedBOnly momentum is conservedCBoth energy and momentum are conservedDNeither energy nor momentum is conservedWhen two bodies collide elastically, then
Akinetic energy of the system alone is conservedBonly momentum is conservedCboth energy and momentum are conservedDneighter energy nor momentum is conservedWhen two bodies collide elastic, then:
AKE of the system along is conservedBonly momentum is conservedCboth KE and momentum are conservedDneither KE nor momentum is conserved
When two bodies collide elastically, the force of interaction between them is
View SolutionIn head on elastic collision of two bodies of equal masses, it is not possible :
View SolutionWhen two spheres of equal masses undergo glancing elastic collision with one of them at rest after collision they will move
View SolutionTwo balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
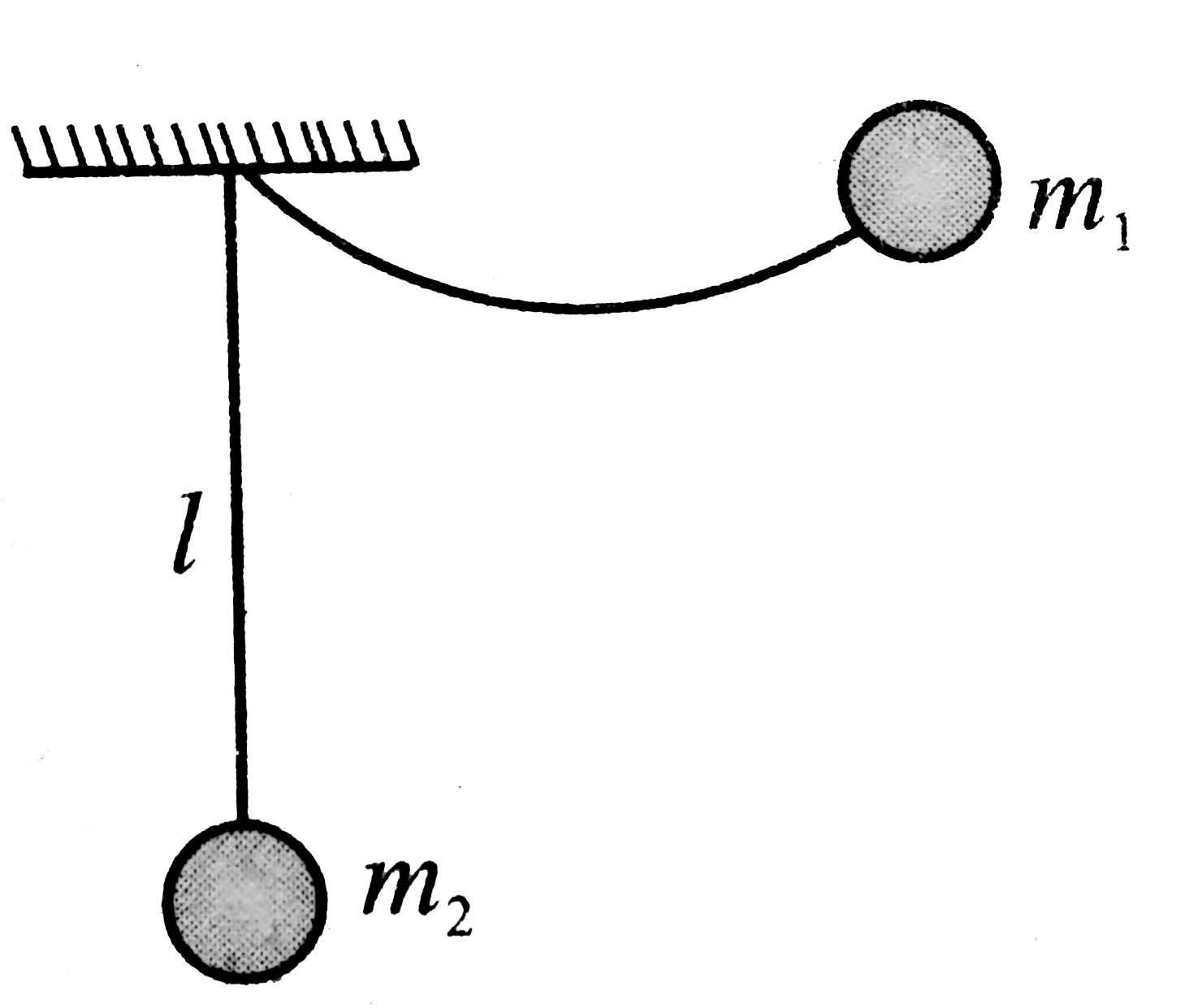
Velocity u1 with which the hall of mass m1 collides with the other ball is
View SolutionIf a body of mass m collides head on, elastically with velocity u with another identical boday at rest. After collision velocty of the second body will be
View Solution

