Let ABCD be a parallelogram such that −−→AB=→q,−−→AD=→pand∠BAD be an acute angle. If →r is the vector that coincides with the altitude direacted from the vertex B to the side AD, then →r is given by : Solution in Kannada
→r=3→q−3(→p.→q)(→p.→p)→p
→r=−→q+→p.→q→p→p)→p
→r=→q−(→p.→q→p.→p)→p
→r=−3→q+3(→p.→q)(→p.→p)→p
The correct Answer is:B
Step by step video, text & image solution for Let ABCD be a parallelogram such that vec(AB)=vecq,vec(AD)= vecp and angle BAD be an acute angle. If vecr is the vector that coincides with the altitude direacted from the vertex B to the side AD, then vecr is given by : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR ALGEBRA Book:MODERN PUBLICATIONChapter:VECTOR ALGEBRA Exercise:RECENT COMPETITIVE QUESTION
Explore 11 Videos
- VECTOR ALGEBRA Book:MODERN PUBLICATIONChapter:VECTOR ALGEBRA Exercise:Multiple Choice Question (Level-II)
Explore 38 Videos
- UNIT TEST PAPER NO.3Book:MODERN PUBLICATIONChapter:UNIT TEST PAPER NO.3Exercise:ASSERTION-REASON & COLUMN MATCHING TYPE QUESTIONS (SECTION-B COLUMN MATCHING TYPE QUESTIONS)
Explore 4 Videos
Similar Questions
A space vector makes the angle 150∘and60∘with the positive direction of x and y-axes. The angle made by the vector with the positive direction of z-axis is :
View SolutionIf →a,→b and →c are three non-coplanar vectors and →p,→q and →r are vectors defined by →p=→b×→c[→a→b→c],→q=→c×→a[→a→b→c] and →r=→a×→b[→a→b→c] , then the value of (→a+→b)⋅(→b+→c)⋅→q+(→c+→a)⋅→r =
View SolutionList-IList-II(A)If mean of 27, 31, 89, 107, 156 is 82, then mean of 130, 126, 68, 50, 1 is(i)√2(B)S. D. of scores 1, 2, 3, 4, 5 is(ii)n+12(C)If mode is 18 and mean is 24, then median is(iii)75(D)Mean of first n natural number is(iv)22
View SolutionLet ABCD be a parallelogram such that vec AB=vec q,vec AD=vec p and /_BAD be an acute angle.If vec r is the vector that coincides with the altitude directed from the vertex B to the side AD,then vec r is
View SolutionvecP,vecQ,vecR,vecS are vector of equal magnitude. If vecP+vecQ-vecR=0 angle between vecP and vecQ is theta_(1) .If vecP+vecQ-vecS=0 angle between vecP and vecS is theta_(2) .The ratio of theta_(1) to theta_(2) is
View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
View SolutionIf vecP+vecQ=vecR" & "vecR is perpendicular to vecP . define angle between vecP" & "vecQ" if " vec|P|=vec|R|-
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
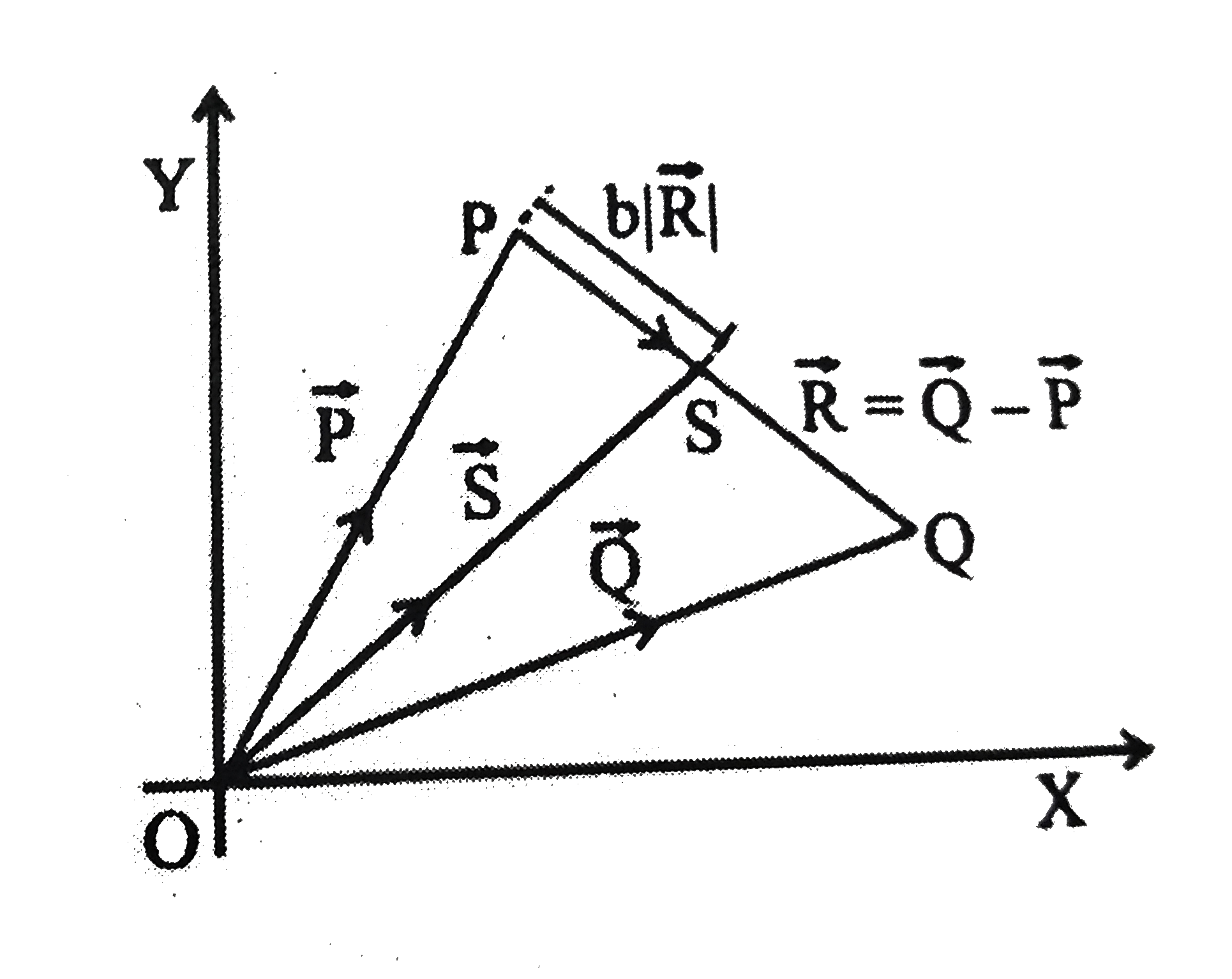
View SolutionIf vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
View SolutionTwo adjacent sides of a parallelogram ABCD are given by −−→AB=2ˆi+10ˆj+11ˆk and −−→AD=−ˆi+2ˆj+2ˆk. The side AD is rotated by an acute angle α in the plane of the parallelogram so that AD becomes AD'. If AD' make a right angle withe the side AB then the cosine of the angle α is given by
View SolutionLet ABCD be a parallelogram such that −−→AB=→q,−−→AD=→Pand∠BAD be an acute angle. If →r is the vector that coincides with the altitude directed from the vertex B to the side AD, then →r is given by-
View SolutionLet ABCD be a parallelogram such that and ∠BAD be an acute angle if →r is the vector that coincides with the altitude directed from the vertex B to the side AD then →r is given by
View Solutionধরা যাক,ABCD সামান্তরিক এরূপ যে −−→AB=→q,−−→AD=→p এবং ∠BAD হল সূক্ষ্মকোণ। যদি →r ভেক্টর B শীর্ষ থেকে AD বাহুর দিকে উচ্চতার সাথে সমাপতিত হয়, তবে →r হল-
View SolutionIf →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
View Solution
