If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
A
Cos−1(512)
B
Cos−1(513)
C
Cos−1(1213)
D
Cos−1(213)
Video Solution
Text Solution
The correct Answer is:C
→P+→Q=→R and P2+Q2=R2
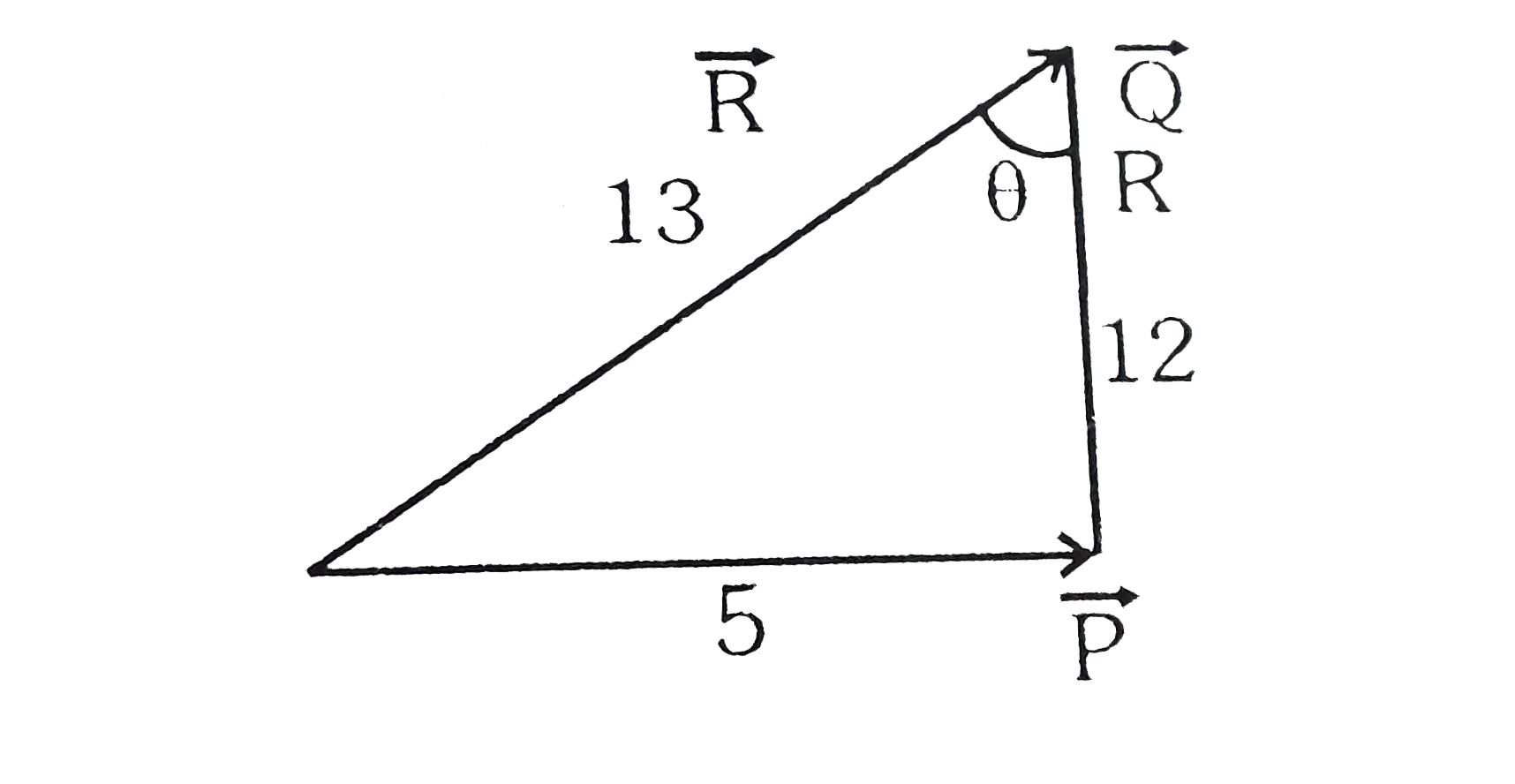
cosθ=1213⇒θ=cos−1(1213)
|
Topper's Solved these Questions
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:EXERCISE-2
Explore 80 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:EXERCISE-3
Explore 20 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Question
Explore 1 Video
- AIIMS 2019Book:ALLENChapter:AIIMS 2019Exercise:PHYSICS
Explore 40 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
Similar Questions
Knowledge Check
If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
Acos−1(512)Bcos−1(513)Ccos−1(1213)Dcos−1(213)If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
ACos−1(512)BCos−1(513)CCos−1(1213)DCos−1(213)If →P.→Q=PQ then angle between →P and →Q is
A0∘B30∘C45∘D60∘
if →P+→Q=→P−→Q, then
View SolutionIf →P−→Q−→R=0 and the magnitudes of →P,→Qand→R are 5 , 4 and 3 units respectively, the angle between →Pand→R is
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
View Solutionif ∣∣→P+→Q∣∣=∣∣→P∣∣+∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View SolutionThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View Solution