The resultant of →P and →Q is perpendicular to →P. What is the angle between →P and →Q
A
(P2−Q22PQ)
B
Q
C
PQ
D
P+QP−Q
Video Solution
Text Solution
The correct Answer is:B
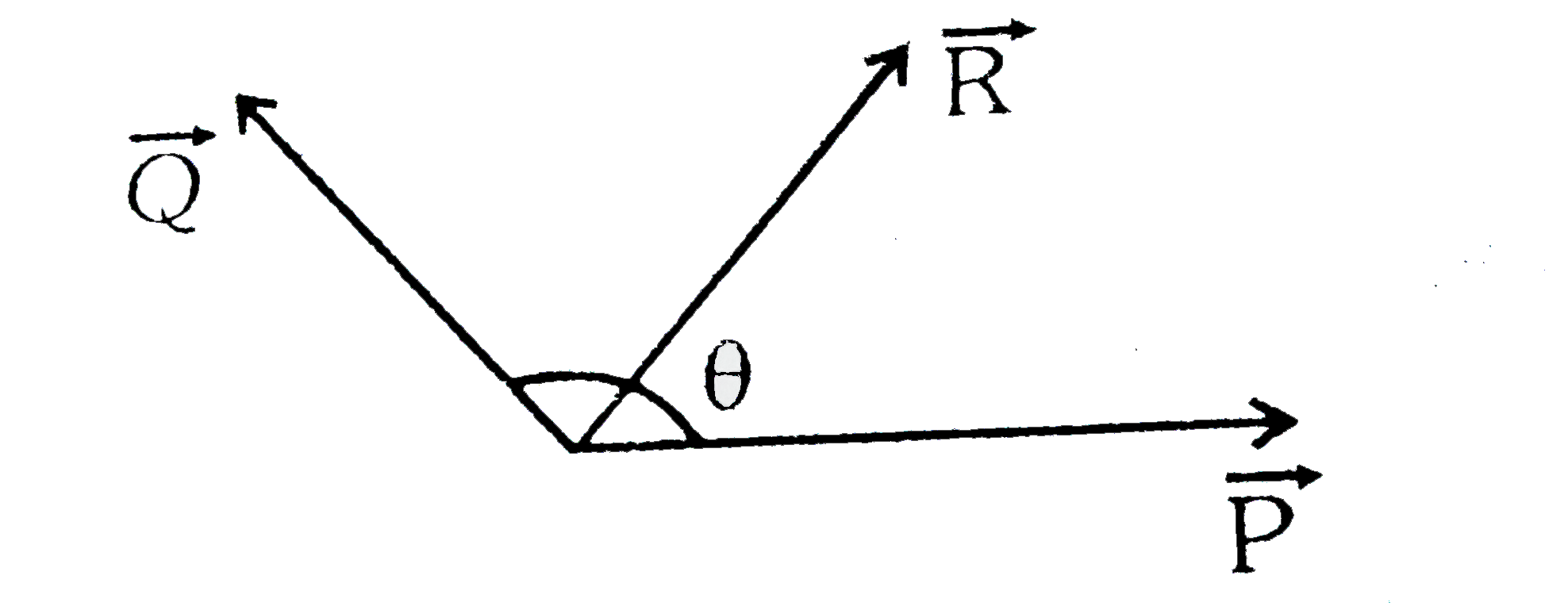
R2=P2+Q2+2PQcosθ

tanα=2Qsinθ{+2Qcosθ)=∞
cosθ=−P2Q
R2=P2+Q2+2PQ(−P)2Q⇒R=Q
|
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-2
80 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-3
20 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Video
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
If →P.→Q=PQ then angle between →P and →Q is
A0∘B30∘C45∘D60∘What is the angle between (→P+→Q) and (→P×→Q)
A0Bπ2Cπ4Dπ radianTwo vectors →P and →Q that are perpendicular to each other are :
A→P=3ˆi+3ˆj+2ˆk,→Q=2ˆi−2ˆj+2ˆkB→P=2ˆi+3ˆj+2ˆk,→Q=2ˆi−2ˆj+2ˆkC→P=2ˆi−3ˆj+2ˆk,→Q=2ˆi−2ˆj−2ˆkD→P=ˆi−3ˆj+2ˆk,→Q=2ˆi−2ˆj+ˆk
If two vectors →P and →Q is chosen such that their resultant is perpendicular to →P . The angle between →P and →Q is cos−1(−nP2Q). Then value of n is:
View SolutionThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
View SolutionIf →P+→Q=→R & →R is perpendicular to →P.
define angle between →P & →Q if −→|P|=−→|R|−
View SolutionIf →P−→Q−→R=0 and the magnitudes of →P,→Qand→R are 5 , 4 and 3 units respectively, the angle between →Pand→R is
View Solution