A uniform electric field of magnitude E = 100 kV/m is directed upward. Perpendicular to E and directed out of the page, there exists a uniform magnetic field of magnitude B = 0.5 T. A beam of particles of charge + q enters this region. What should be the chosen speed of the particles for which the particles will not be deflected by the crossed electric and magnetic field? Assume that the particles are moving in +ve direction.
To solve the problem, we need to find the speed of the charged particles such that they experience no net force and thus are not deflected by the crossed electric and magnetic fields.
1. Identify the Forces Acting on the Particles:
- The electric force (FE) acting on the charged particles due to the electric field E is given by:
FE=qE
- The magnetic force (FB) acting on the charged particles due to the magnetic field B is given by:
FB=q(v×B)
2. Determine the Directions of the Fields:
- The electric field E is directed upward (let's say in the positive y-direction).
- The magnetic field B is directed out of the page (let's say in the positive z-direction).
- The velocity v of the particles is in the positive x-direction.
3. Calculate the Magnetic Force:
- The magnetic force can be calculated using the right-hand rule for the cross product v×B:
- v is in the i direction (positive x-axis).
- B is in the k direction (positive z-axis).
- The cross product v×B gives:
v×B=i×k=−j
- Therefore, the direction of the magnetic force FB is in the negative y-direction.
4. Set the Forces Equal for No Deflection:
- For the particles to not be deflected, the electric force must equal the magnetic force in magnitude:
FE=FB
- Substituting the expressions for the forces:
qE=qvB
5. Simplify the Equation:
- We can cancel q from both sides (assuming q≠0):
E=vB
6. Solve for the Velocity v:
- Rearranging the equation gives:
v=EB
- Substituting the given values:
- E=100kV/m=100×103V/m
- B=0.5T
v=100×1030.5=200×103m/s=2×105m/s
7. Final Answer:
- The speed of the particles should be v=2×105m/s.
- The electric force (FE) acting on the charged particles due to the electric field E is given by:
FE=qE
- The magnetic force (FB) acting on the charged particles due to the magnetic field B is given by:
FB=q(v×B)
- The electric field E is directed upward (let's say in the positive y-direction).
- The magnetic field B is directed out of the page (let's say in the positive z-direction).
- The velocity v of the particles is in the positive x-direction.
- The magnetic force can be calculated using the right-hand rule for the cross product v×B:
- v is in the i direction (positive x-axis).
- B is in the k direction (positive z-axis).
- The cross product v×B gives:
v×B=i×k=−j
- Therefore, the direction of the magnetic force FB is in the negative y-direction.
- For the particles to not be deflected, the electric force must equal the magnetic force in magnitude:
FE=FB
- Substituting the expressions for the forces:
qE=qvB
- We can cancel q from both sides (assuming q≠0):
E=vB
- Rearranging the equation gives:
v=EB
- Substituting the given values:
- E=100kV/m=100×103V/m
- B=0.5T
v=100×1030.5=200×103m/s=2×105m/s
- The speed of the particles should be v=2×105m/s.
Topper's Solved these Questions
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Solved Problems (Subjective)
10 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Solved Problems (Objective)
14 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
- MAGNETISMBOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example
12 Videos
Similar Questions
A charged particle enters into a uniform magnetic field and experiences upward force as indicated in figure. What is the charge sign on the particle?
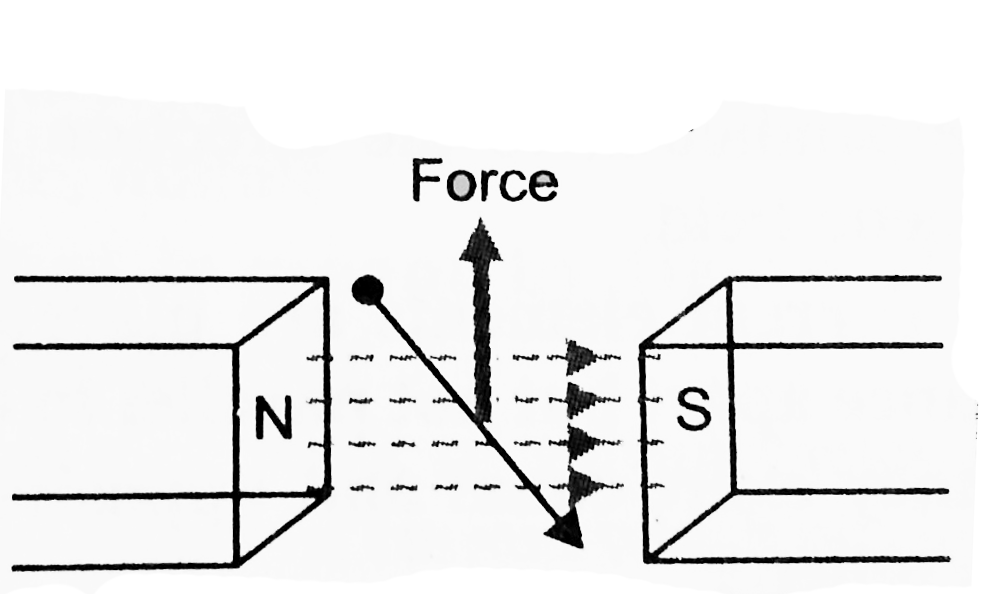
View SolutionA charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force . The path of the particle is a circle .
View Solution
Knowledge Check
A charged particle moving with velocity vis subjected to electric field E and magnetic field B. The particle will go undeflected if
AE is perpendicular to B.BE is parallel to v and perpendicular to B.CE and B both are parallel to v.DE, B and v are mutually perpendicular but v=EB.A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
Aincreases the K.E. of the particleBdecreases the K.E. of the particleCchanges the direction of motion of the particleDdoes both (a) and ( c)There is a uniform magnetic field and a charged particle is given an initial velocity at an acute angle to the direction of the magnetic field. What kind of path will the particle follow?
ACircleBStraight lineCHelical path with a non-uniform pitch.DHelical path with a uniform pitch.
In a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
View SolutionIf a beta particle enters in magnetic and electric field with its velocity pointing in the same direction as electric and magnetic field then :
View SolutionA particle enters the region of a uniform magnetic field as shown in figure. The path of the particle inside the field is shown by dark line. The particle is :

View Solution
