Two magnets of moment M and 2 M are tied at an angle of 60∘ to each other . What is the resultant magnetic moment of the combination ?
To find the resultant magnetic moment of two magnets with moments M and 2M tied at an angle of 60∘ to each other, we can use the formula for the resultant of two vectors. Here are the steps to solve the problem:
1. Identify the Magnitudes and Angle:
- Let the magnetic moment of the first magnet be M1=M.
- Let the magnetic moment of the second magnet be M2=2M.
- The angle between the two magnets is given as θ=60∘.
2. Use the Formula for Resultant Magnetic Moment:
- The formula for the resultant magnetic moment Mr when two magnetic moments are at an angle θ is:
Mr=√M21+M22+2M1M2cosθ
3. Substitute the Values into the Formula:
- Substitute M1=M, M2=2M, and θ=60∘ into the formula:
Mr=√M2+(2M)2+2⋅M⋅2M⋅cos60∘
4. Calculate Each Term:
- Calculate (2M)2=4M2.
- Calculate cos60∘=12.
- Substitute these values into the equation:
Mr=√M2+4M2+2⋅M⋅2M⋅12
- This simplifies to:
Mr=√M2+4M2+2M2=√7M2
5. Final Result:
- Take the square root:
Mr=√7M
Conclusion:
The resultant magnetic moment of the combination is Mr=√7M.
---
- Let the magnetic moment of the first magnet be M1=M.
- Let the magnetic moment of the second magnet be M2=2M.
- The angle between the two magnets is given as θ=60∘.
- The formula for the resultant magnetic moment Mr when two magnetic moments are at an angle θ is:
Mr=√M21+M22+2M1M2cosθ
- Substitute M1=M, M2=2M, and θ=60∘ into the formula:
Mr=√M2+(2M)2+2⋅M⋅2M⋅cos60∘
- Calculate (2M)2=4M2.
- Calculate cos60∘=12.
- Substitute these values into the equation:
Mr=√M2+4M2+2⋅M⋅2M⋅12
- This simplifies to:
Mr=√M2+4M2+2M2=√7M2
- Take the square root:
Mr=√7M
The resultant magnetic moment of the combination is Mr=√7M.
Topper's Solved these Questions
- MAGNETISM AND MATTERBook:FIITJEEChapter:MAGNETISM AND MATTERExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE ) (LEVEL -1)
Explore 18 Videos
- MAGNETISM AND MATTERBook:FIITJEEChapter:MAGNETISM AND MATTERExercise:ASSIGNMENT PROBLEMS OBJECTIVE : (LEVEL -I) (MULTI CHOICE SINGLE CORRECT)
Explore 21 Videos
- MAGNETISM AND MATTERBook:FIITJEEChapter:MAGNETISM AND MATTERExercise:SOLVED PROBLEMS OBJECTIVE : (LEVEL - II)
Explore 10 Videos
- MAGNETISMBook:FIITJEEChapter:MAGNETISMExercise:Example
Explore 12 Videos
- MODERN PHYSICSBook:FIITJEEChapter:MODERN PHYSICSExercise:Numerical based questions
Explore 5 Videos
Similar Questions
Two bar magnets of magnetic moments M1 and M2 are placed at an angle with each other. What will be the resultant dipole moment, if
(1) like poles are placed at the same location? (2) unlike poles are placed at the same location?
View SolutionWhat is the theoretical magnetic moment of Ti3+ ion ?
View Solution
Knowledge Check
A magnet of length 14cm and magnetic moment μ is broken into two parts of length 6 cm and 8 cm. They are put at right angles to each other with the opposite poles togather. The magnetic dipole moment of the combination is:
Aμ/1.4BμC1.4μD2.8μThe magnetic moment (B.M) of Fe2+ ion is
A0B√35C√24D2√2If two identical bar mangets, each of length 'I', pole strength 'm' and magnetic moment 'M' are placed perpendicular to each other with their unlike poles in contact, the magnetic moment of the combination is
AM√2Blm(√2)C2lm(√2)D2M
Two bar magnets each of magnetic moments M are placed at an angle 60∘ with each other. Calculate the resultant dipole moment, if (a) like poles are placed at the same location (b) unlike poles are placed at the same location
View SolutionThree equal magnetic moments are arranged as shown in the figure. What will be the resultant magnetic moment of this combination?

View SolutionTwo identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
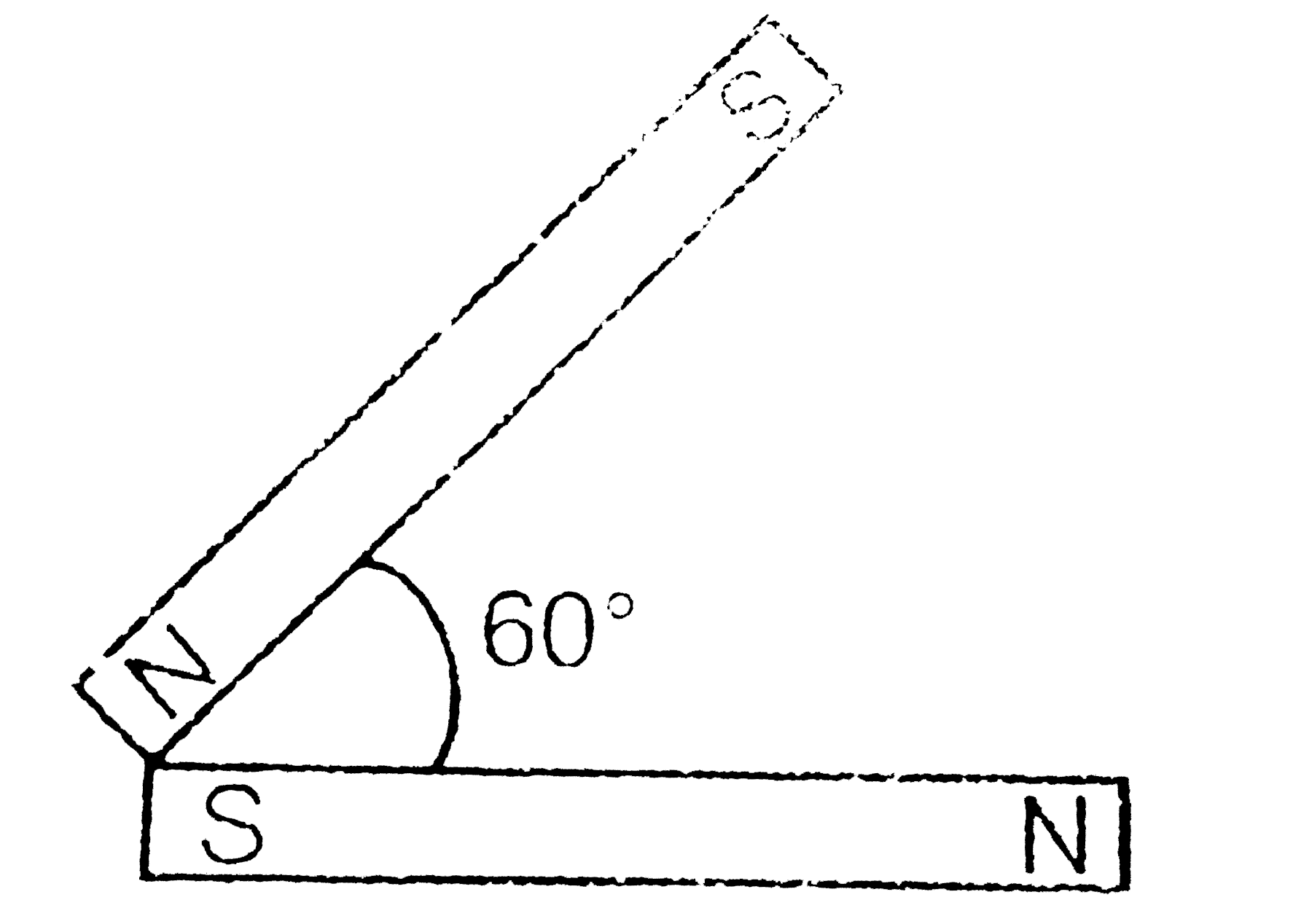
View SolutionTwo magnets of magnetic moments 4Am2and3Am2 are joined to form a cross (+), then the magnetic moment of the combination is
View SolutionA magnetised wire of moment M is bent into an arc of a circle subtending an angle of 60^(@) at the centre. The new magnetic moment is

View Solution

