A cabin is moving in a gravity free space along y-axis with an acceleration a. What is the time period of oscillation of a particle of mass m attached with an inextensible string of length l, in this cabin
2π√lg
2π√la
2π√la+g
2π√lg−a
The correct Answer is:B
In gravity free space g = 0
Tension in the string at equilibrium position =ma
Effective g = a
And thus T=2π√la
Hence (B) is correct
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:COMPREHENSION
Explore 17 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assertion Reason type
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Solved Problems (Subjective)
Explore 13 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
A particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
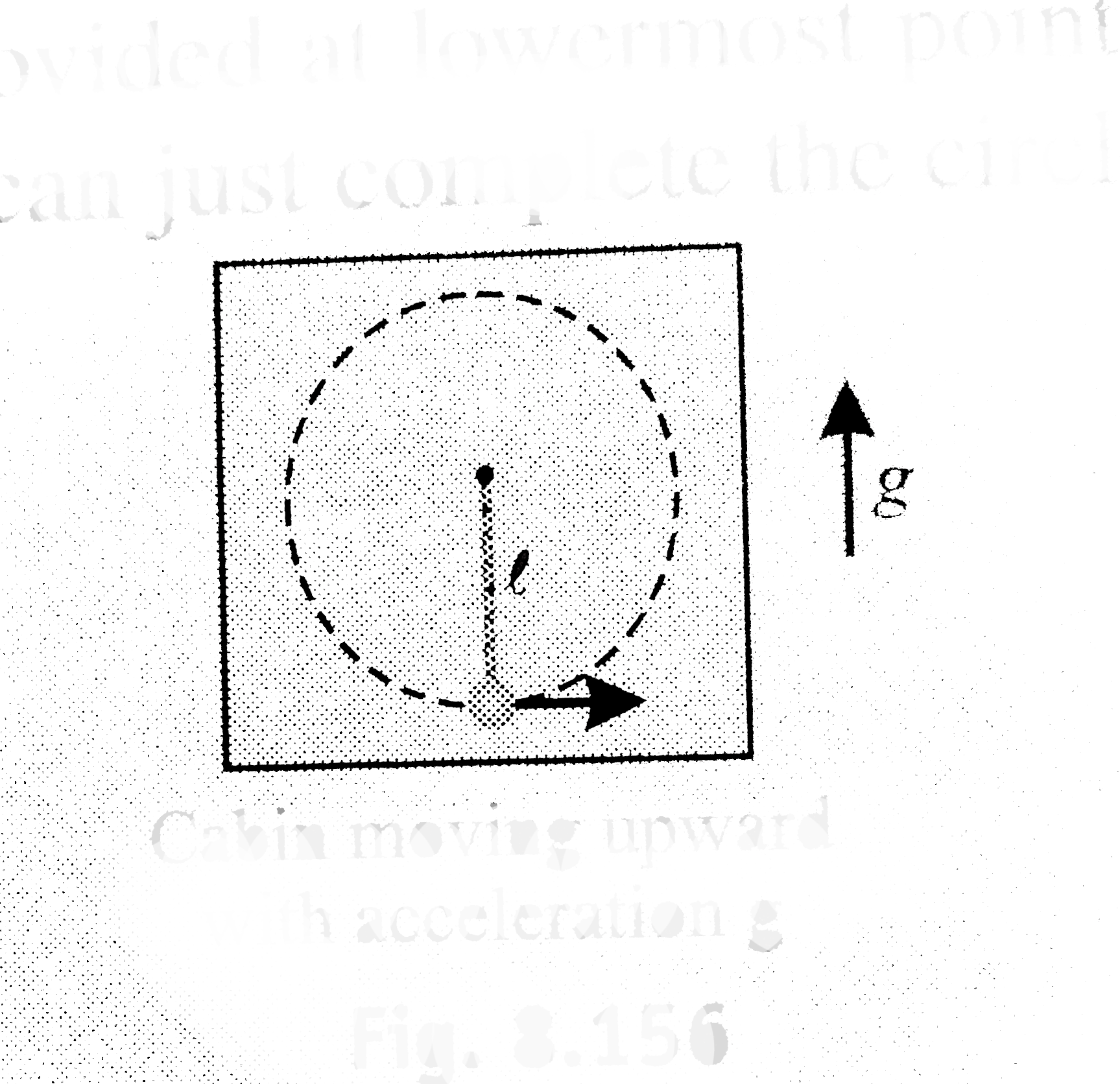
View Solution
Knowledge Check
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2mA cabin is falling freely under gravity, what is the time period of a pendulum attached to its celling?
AzeroB∞C1 sD2 sA particle moves along the X-axis according to to the law S=asin2(ωt−π/4)
The time period of oscillations isA2πwBT/WC3π2WDπ2W
A pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
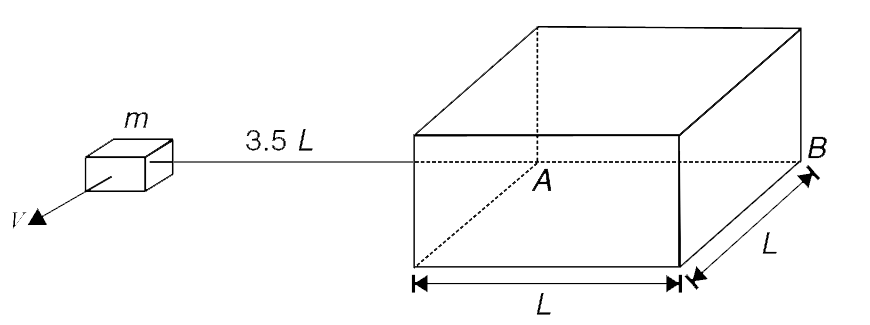
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.

View SolutionThree spring mass systems are shown in figure. Assuming gravity free spece, find the time period of oscillations in each case. What should be the answer if space is not gravity free ?
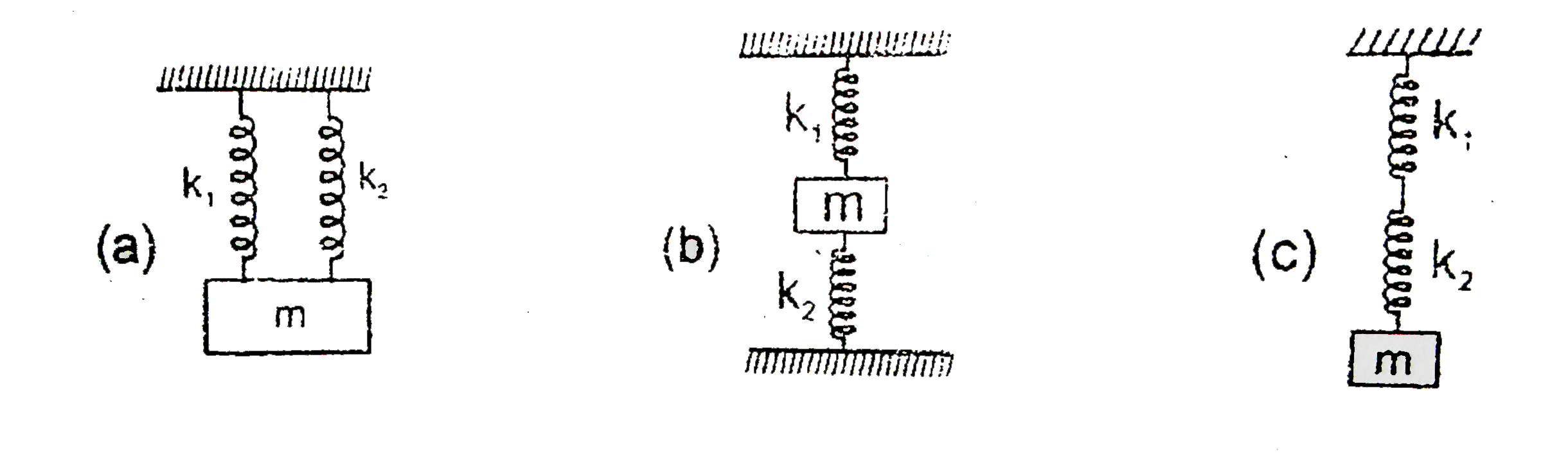
View SolutionThree spring mass systems are shown in figure. Assuming gravity free spece, find the time period of oscillations in each case. What should be the answer if space is not gravity free ?
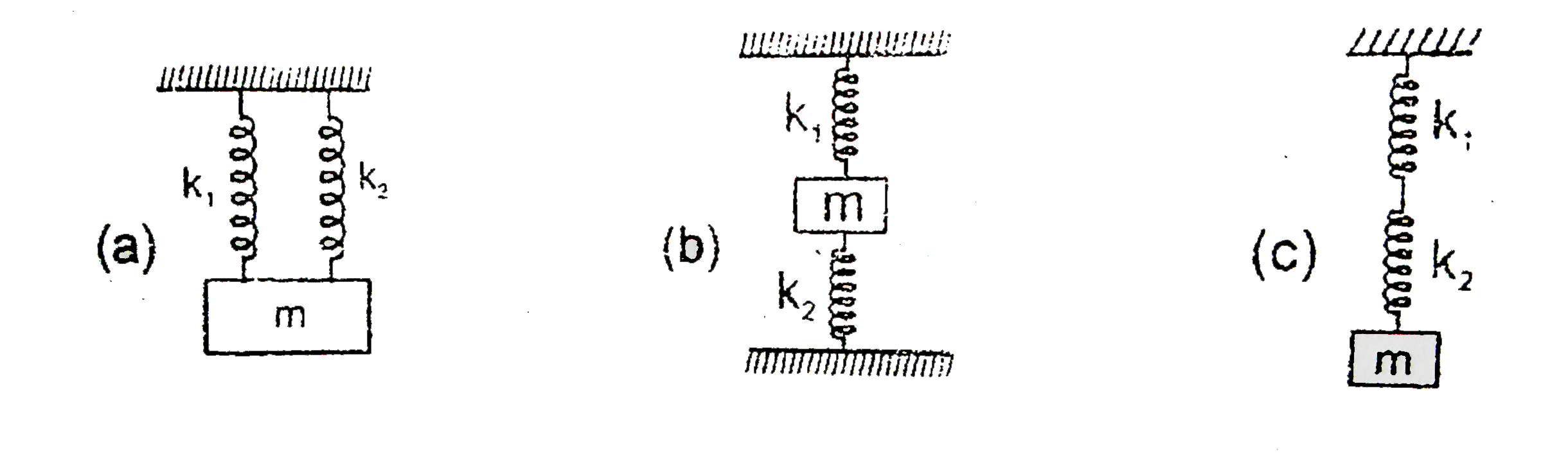
View SolutionA ring of mass m free to slide on a fixed smooth horizontal rod is attached to a particle of mass M kg by a inextensible string of length l. Initially, both M and m are at rest and the string is vertical. A horizontal velocity v0 is imparted to the particle. The maximum height up to which block will rise w.r.t its initial position is (M = 2m)
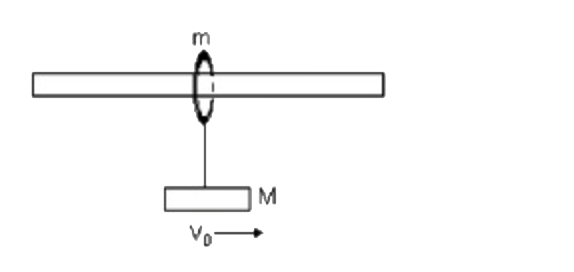
View Solution

