A uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
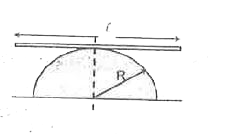
The net torque acting on the bar about P when it is tilte through a small distance x (corresponding angle θ) is given as
τ=−mgxcosθ
⇒−lpω2oscθ=mgx
⇒−ml212ω2osc=mgRθ
cosθ≅1 for small θ&x=Rθ for small θ
⇒ωosc=√12gRl2
⇒T=2πω=2πlω=2πl√12gR=πl√3gR
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Solved Problems (Objective)
Explore 16 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:COMPREHENSION
Explore 17 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
Consider a situation shown in the figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute S.H.M. calculate the time period.

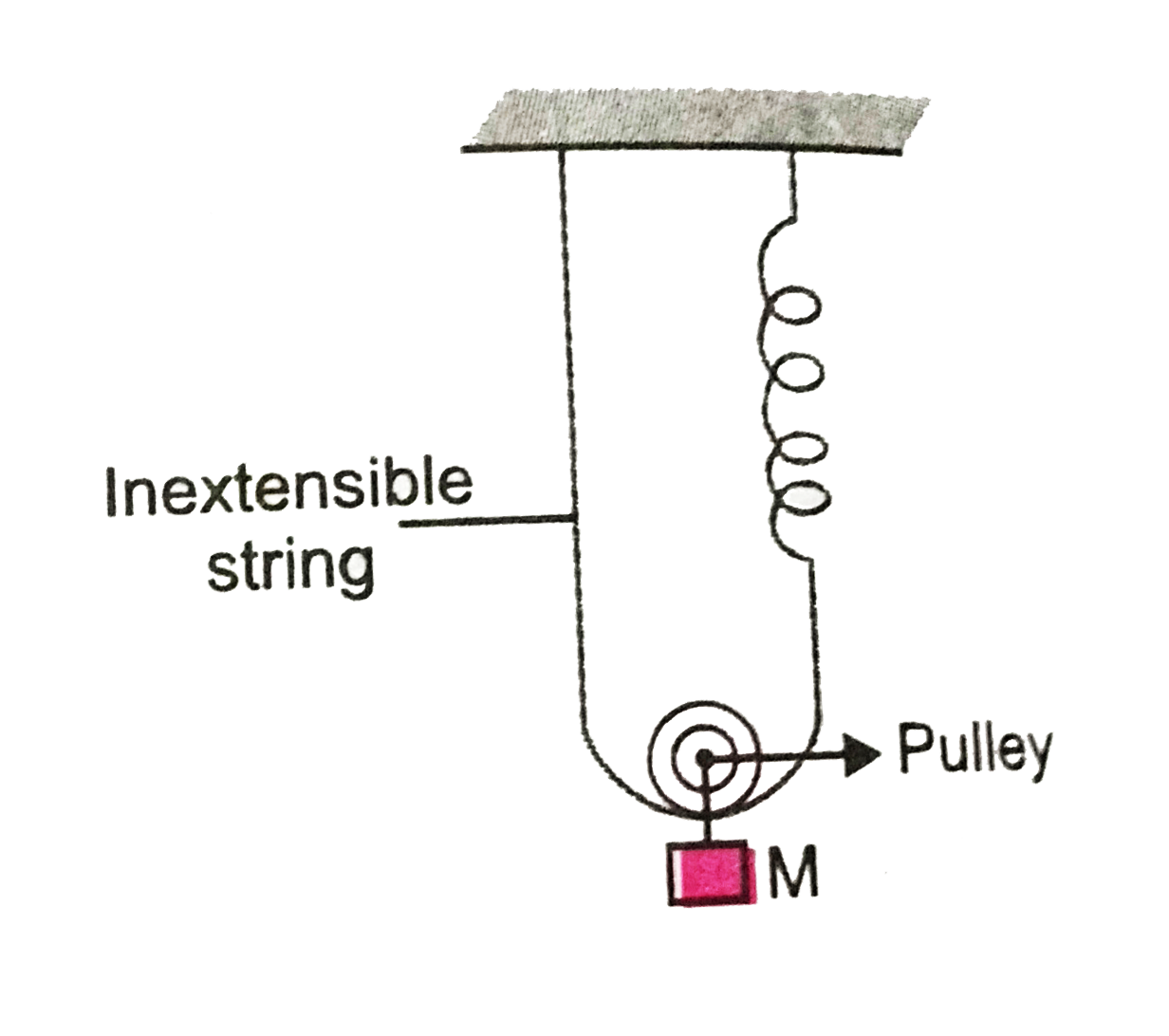
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View Solution
Knowledge Check
A pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
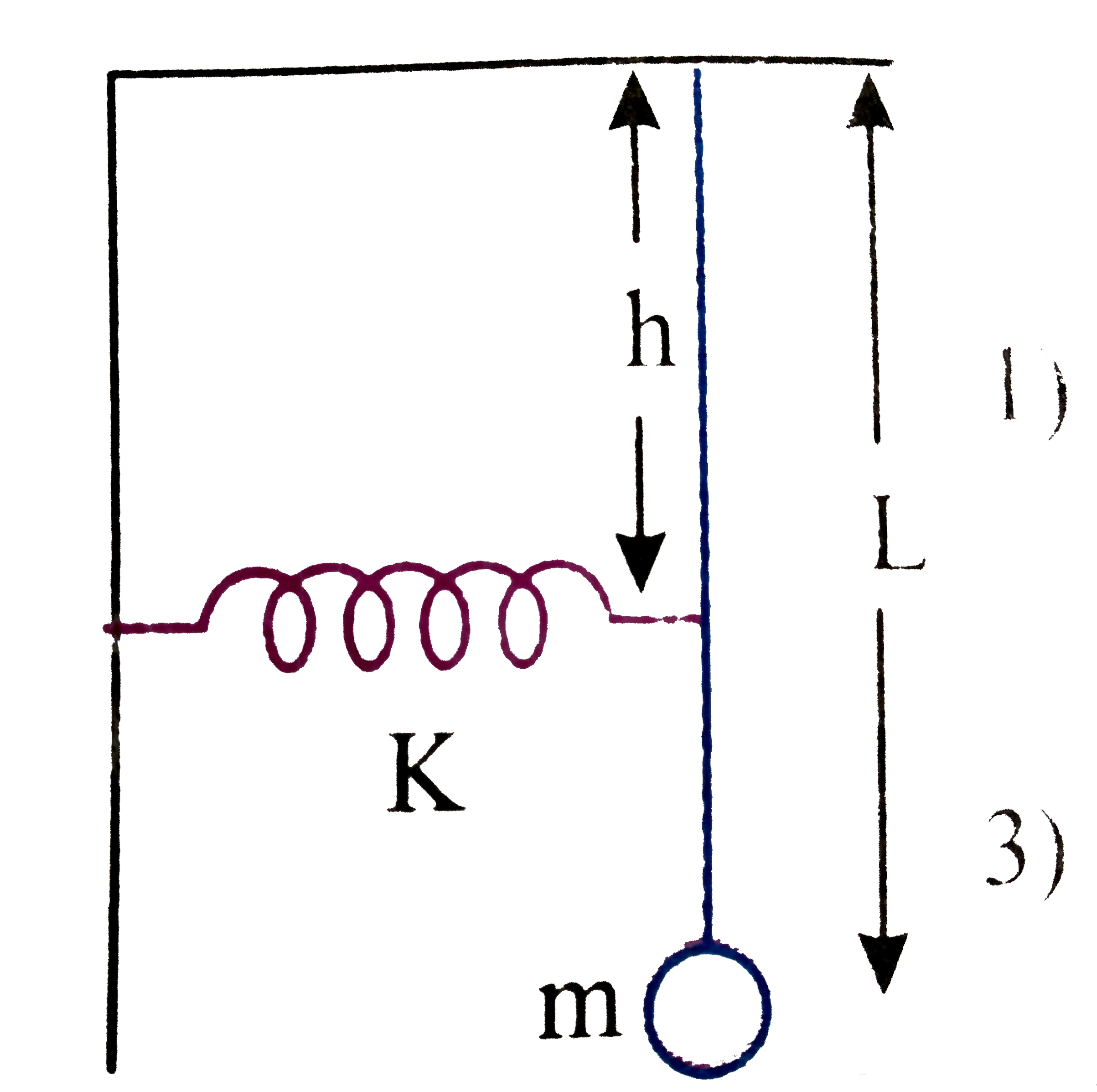 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2A sphere of catius r is kept on a concave of mirror radius of curation R. The arrangement a kept on a horizontal tavke (the surface of concave mirror is fricationless and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes S.h.M. The period of oscillation will be
A2π ⎷((R−r)1.44)B2π√(R−rg)C2π√(rRa)D2π√(Rgr)A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
Find the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
View SolutionA magnetic dipole of magnetic moment M is suspended by a string in a uniform horizontal magnetic field as showo in figure. If in horizontal plane this dipole is slightly tilted and released, show that it will execute simple harmonic motion and find its oscillation period. Consider the dipole as a uniform rod of mass m and length I.
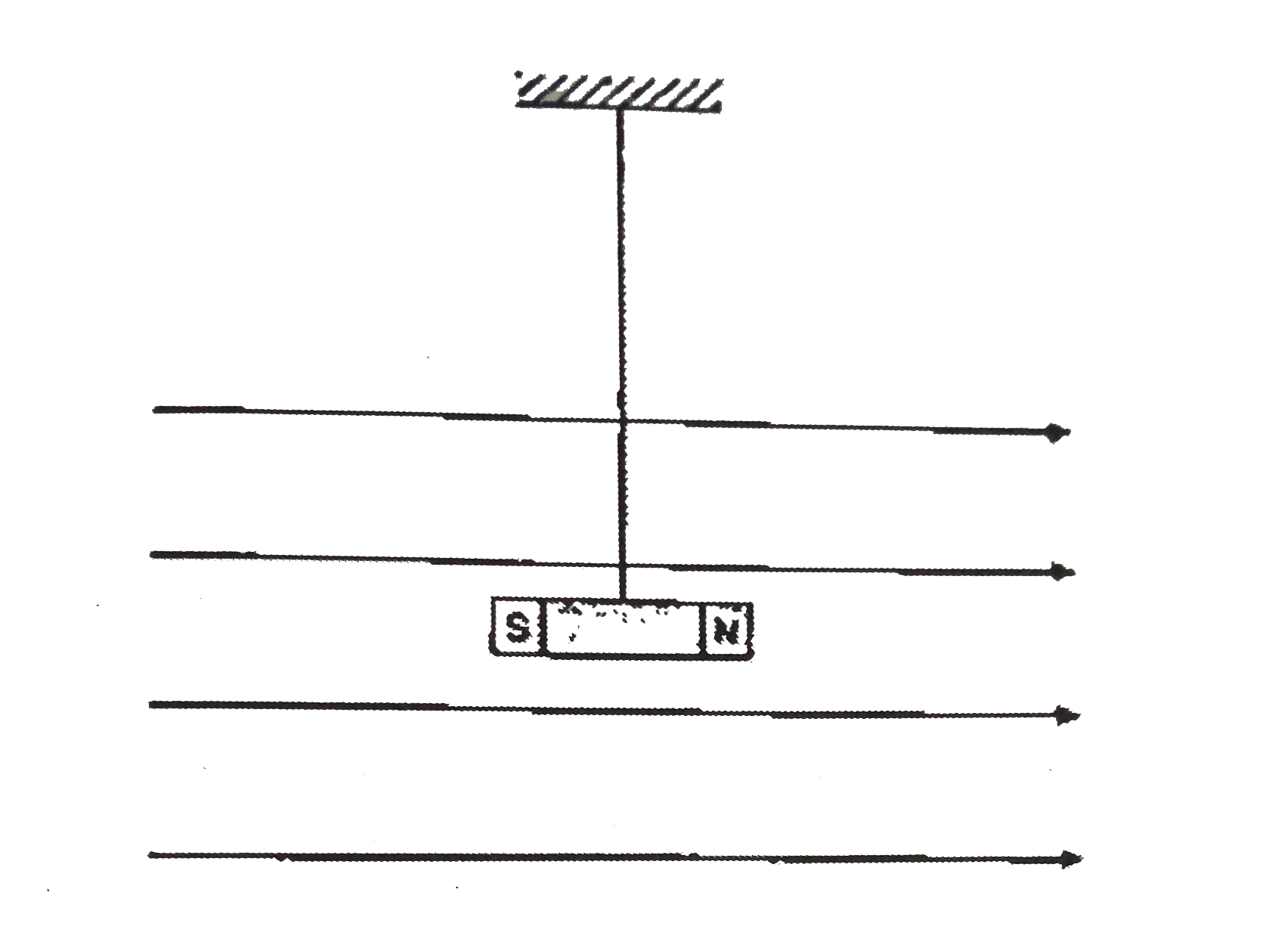
View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these osillations.

View SolutionThe arrangement shown below consists of a uniform metre scale of length 1 m, balanced on a fixed hemisphere of radius 20 cm. when one end of the scale is slightly pressed and released, it performs S.H.M. Determine the angular frequency of oscillations.
(Take g = 10 ms−2)
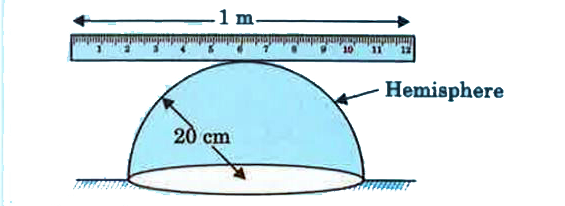
View Solution

