In the given figure all the surfaces are smooth. Find the time taken by the block to reach from the free end to the pulley attached to the plank.
Distance between free end and pulley is l.

Equation of motion for M:
2F=Ma2 ...(1)
For m,
F=ma1 ...(2)
Relative acceleration between M and m=ar=a1+a2
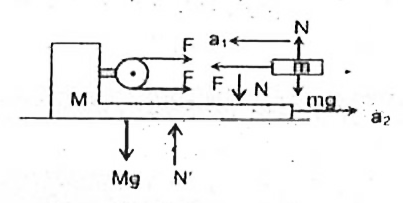
a1+a2=2FM+FM=F[2M+1m] .....(3)
Let the block m strike the pulley after a time t.
Since,
l=12art2
⇒t=
⎷2lF(2M+1M)
⇒t=√2Mml(2m+M)F
Topper's Solved these Questions
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 17 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION - I
Explore 6 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Numerical Based Type
Explore 2 Videos
Similar Questions
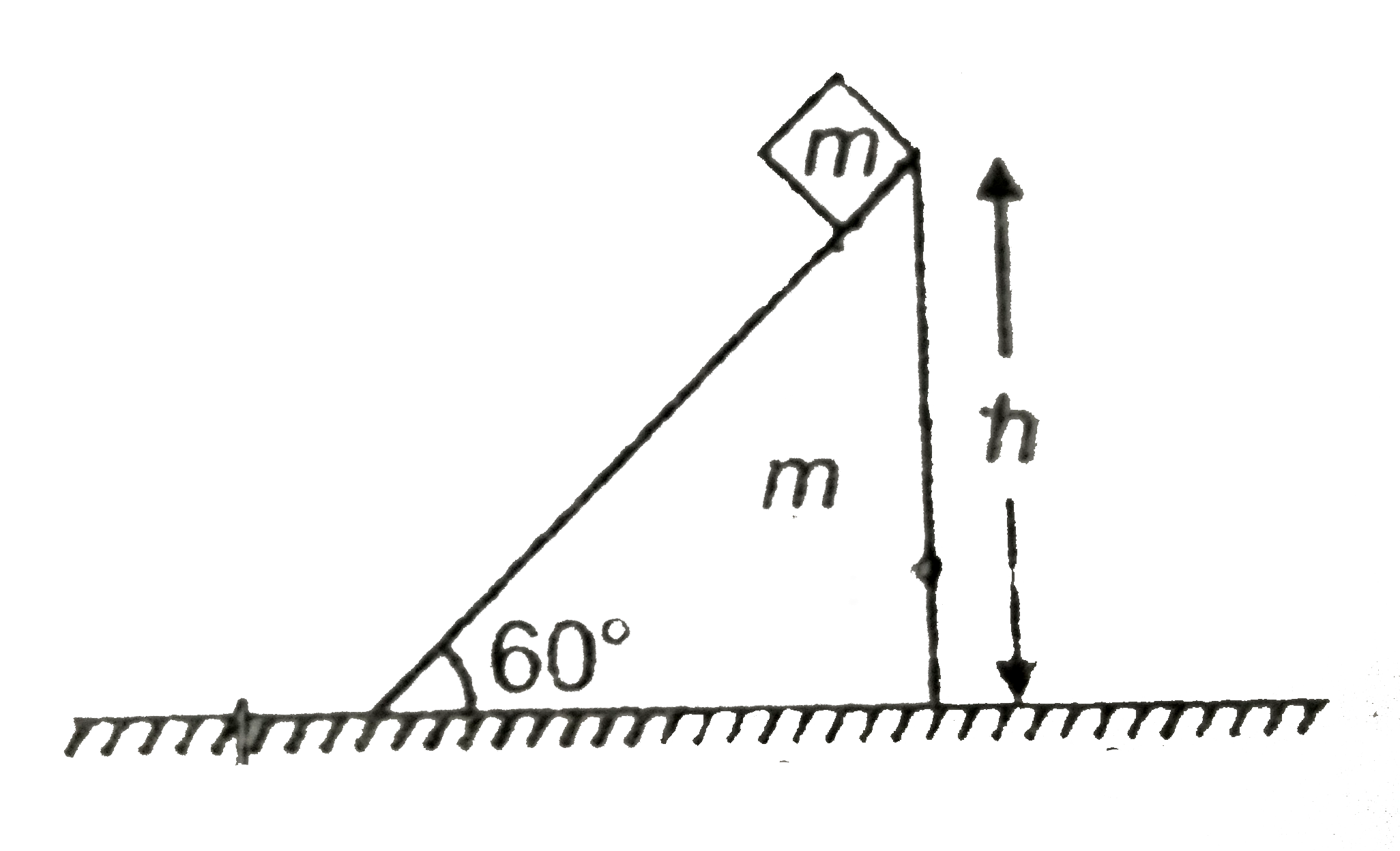
A block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.

View Solution
Knowledge Check
Find the velocity of the hanging block if the velocities of the free ends of the rope are as indicated in the figure.
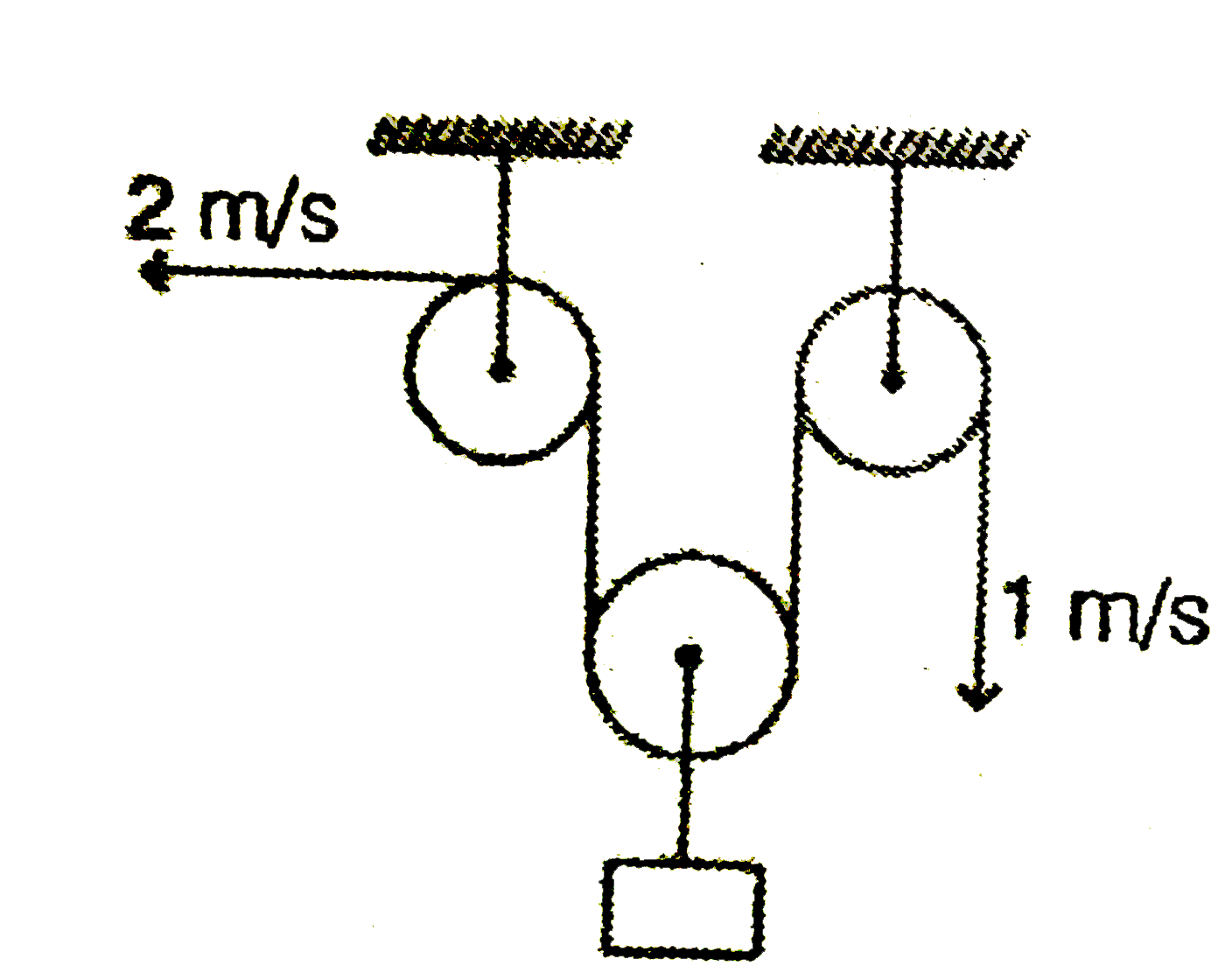 A3/2m/s↑⏐B3/2m/s⏐↓C1/2m/s↑⏐D1/2m/s⏐↓
A3/2m/s↑⏐B3/2m/s⏐↓C1/2m/s↑⏐D1/2m/s⏐↓In the given figure inclined surface and pulleys are smooth. Strings and pulleys are massless. Acceleration of mass m is :
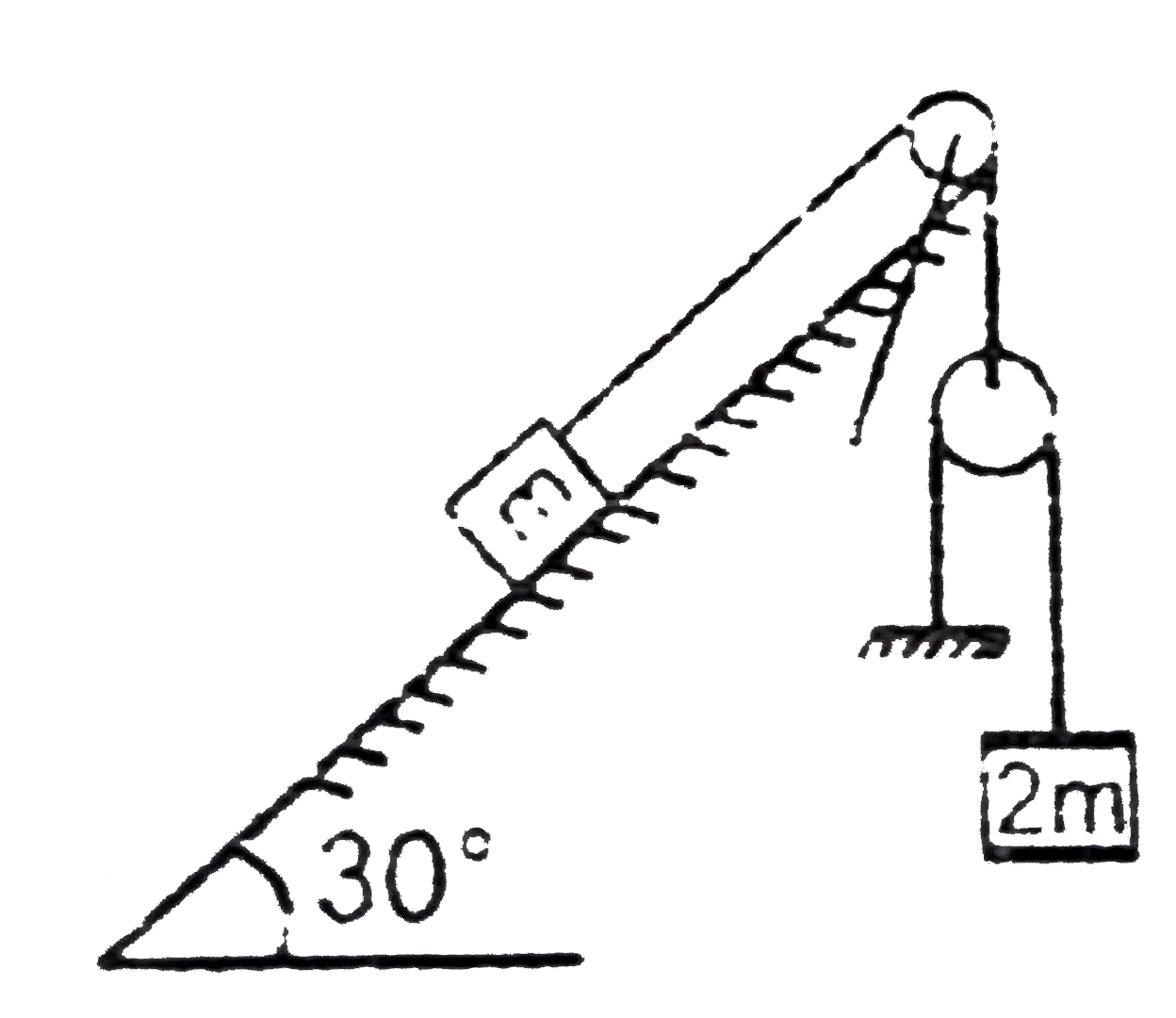 A7g9B7g11C7g18D7g20
A7g9B7g11C7g18D7g20In the above question 63 distance between the man and the block 'A', when man reaches the pulley is:
A10 mB2 mC20 mDNone of these
A plank of mas M and length L is at rest on as frictionless floor. The top surface of the plank has friction. At one end of it a man of mass m is standing as shown in figure. If the man walks towards the other end the find the distance, which the plank moves a till the man reaches the centre of the plank. b. till the man reaches the other end of the plank.

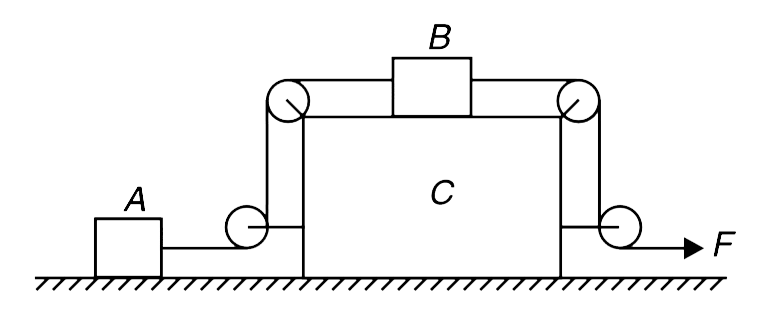
View SolutionIn the system shown in the figure, all surfaces are smooth. Block A and B have mass m each and mass of block C is 2 m. All pulleys are massless and fixed to block C. Strings are light and the force F applied at the free end of the string is horizontal. Find the acceleration of all three blocks.
View SolutionTwo men of masses M and M+m start simultaneously from the ground and climb with uniform accelerations up from the free ends of a massless inextensible rope whick passes over a smooth pulley at a height h from the ground.
(a) Which man reaches the pulley first?
(b) If the mam who reaches first takes time t to reach the pulley, then find the distance of the second man from the pulley at this instant.
View SolutionA particle A of mass 2m is held on a smooth horizontal table and is attached to one end of an inelastic string which runs over a smooth light pulley at the edge of the table. At the other end of the string there hangs another particle B of mass m, the distance from A to the pulley is l. The particle A is then projected towards the pulley with velocity u.

(a) Find the time before the string becomes taut, and shown that after the string becomes taut, the initial velocity of A and B is 4u/3.
(b) Find the common velocity when A reaches the pulley (assume that B has not yet reached the ground).
View SolutionConsider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

View Solution

