A small ball on a frictionless horizontal surface moves towards right with velocity v. It collides with the wall and returns back and continues to and fro motion. If the average speed for first to and fro motion of the ball is (23)v, then the coefficient of restitution of impact is

The ball moves from A to B with a speed v1=v and returns from B to ∧ with a speed v2 say
Since, →v2=−e→v1
⇒v2(−ˆi)=−ev1ˆi
⇒v2=ev1=ev (∵v1=v)
Therefore
→v=AB+BAABv1+BAv2=2v1v2v1+v2
Substituting respective values, we get
v1=v & v2=ev
we obtain,
→v=2v(ev)v+ev=2ev1+e⇒→vv=2e1+e ...(1)
Since, it is given that →v=(2/3)v
⇒→vv=23 ...(2)
Equating (1) and (2), we obtain,
⇒e=0.5.
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 10 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 18 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball P moving with a speed of v ms collides directly with another identical ball Q moving with a speed 10ms' in the opposite direction. P comes to rest after the collision. If the coefficient of restitution is 0.6 the value of v is
View Solution
Knowledge Check
A man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man (for to and fro motion) is :
A0B√uvCu+v2Dv2−u2vA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
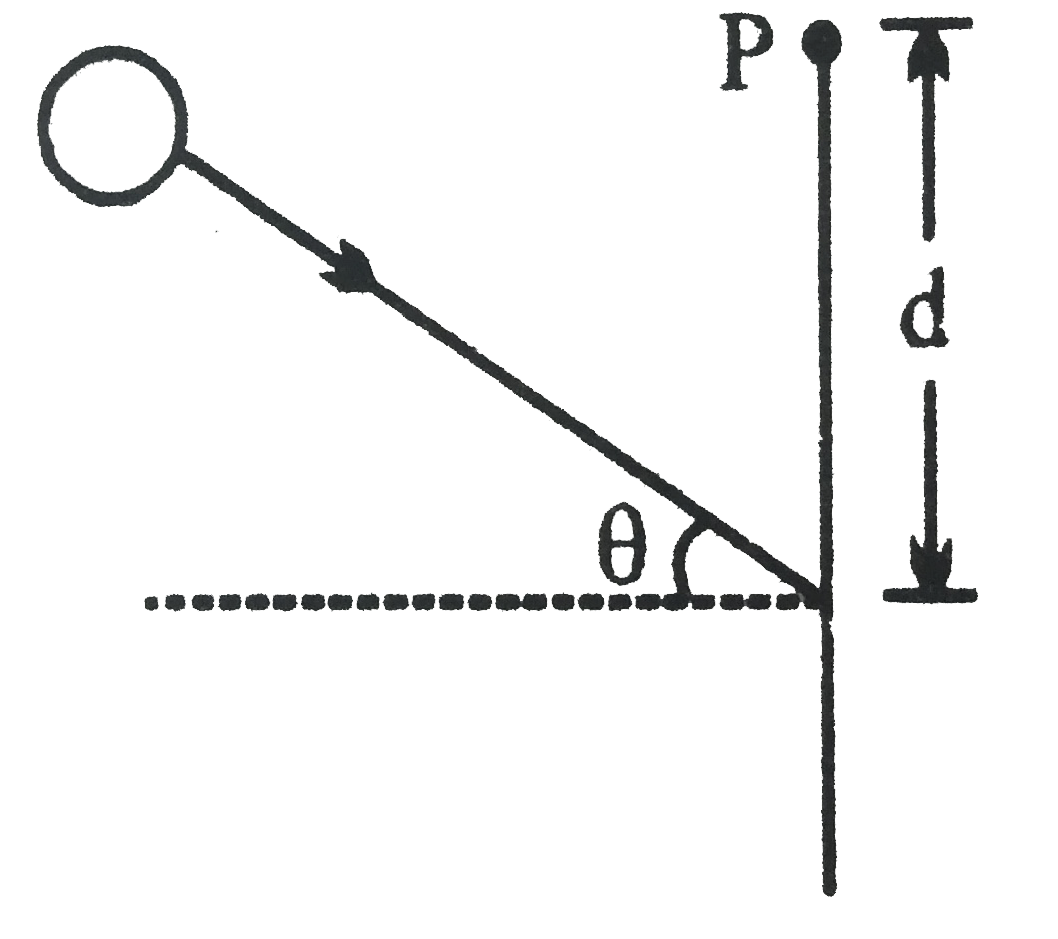 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzeroTwo small balls A and B, each of mass m, are joined rigidly at the ends of a light rod of length L. They are placed on a frictionless horizontal surface. Another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown in the figure. If the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
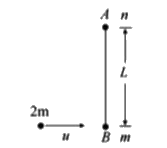 A43ulBulC23ulDnone of these
A43ulBulC23ulDnone of these
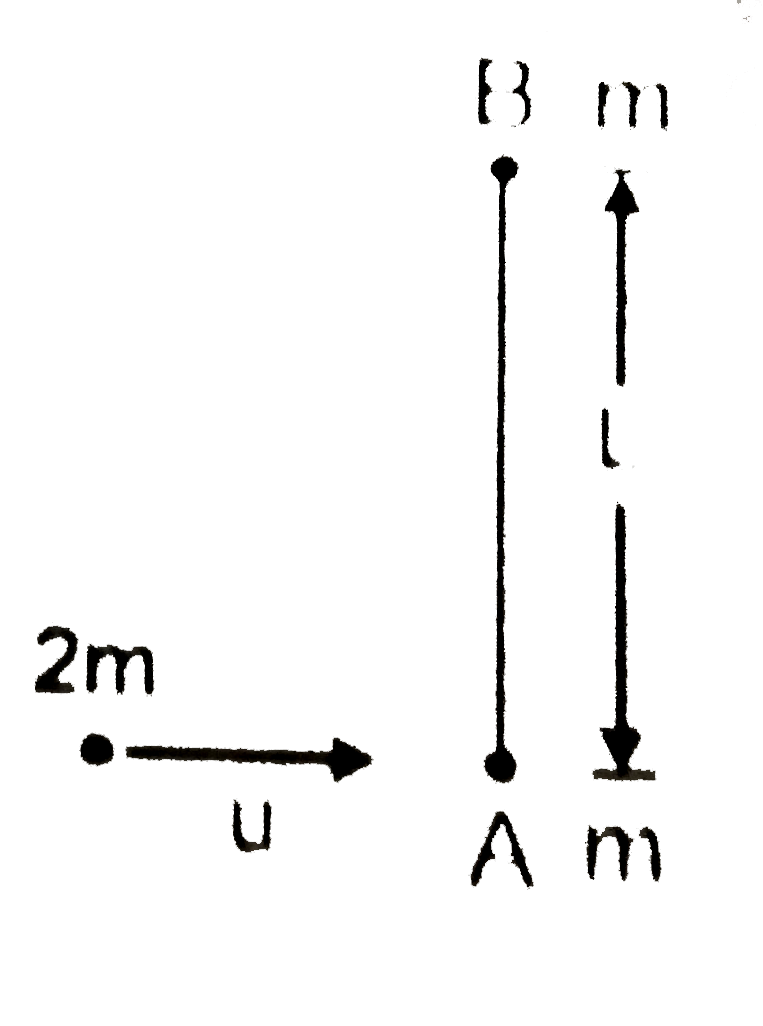
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rof of length L. they are placed on a frictionless horizontal surface another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown int he figure. if the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
View SolutionA ball collides with an inclined plane of inclination θ after falling through a distance h. if it moves horizontal just after the impact, the coefficient of restitution is
View SolutionA ball of mass m moving with a speed v makes a head on collision with an identical ball at rest. The kinetic energy after collision of the balls is three fourth of the original kinetic energy. The coefficient of restitution is
View SolutionA ball A of mass 3m is placed at a distance d from the wall on a smooth horizontal surface Another ball B of mass m moving with velocity u collides with ball A. The coefficient of restitution between the balls and the wall and between the balls is e
(a) the velocity of ball B after collision is u(3e−1)4.
(b) the velocity of ball B after collision is u(2e−1)4.
( c) after collision, ball A will have away by distance d(2e−1)(2e−1) during the time ball B returns back to wall.
(d) after collision, ball A will move away by distance d(e−1)(3e−1) during the time ball B returns back to wall.
View SolutionA body A moves towards a wall with velocity V. The wall also moves towards the body A with velocity V0. After collision the body moves in opposite direction with velocity V∣ which is (1+2V0V) times the velocity V. The coefficient of restitution is
View Solution
