In case of a transverses wave in a string
if λ2π>A0 maximum particle speed is more than the wave speed
if λ2π=A0, particle speed is equal to the wave speed
if λ2π=A0, maximum particle speed is less than wave speed
if λ2π=A0, maximum particle speed may be greater than wave speed
The correct Answer is:B
To solve the problem regarding the relationship between maximum particle speed and wave speed in a transverse wave in a string, we will follow these steps:
1. Understanding Wave Parameters:
- The wave speed (v) is given by the formula:
v=ωk
- The maximum particle speed (v_max) is given by:
vmax=ωA0
where ω is the angular frequency and A0 is the amplitude of the wave.
2. Relating Wavelength and Wave Number:
- The wave number k is defined as:
k=2πλ
- Therefore, substituting k into the wave speed formula gives:
v=ω2πλ=ωλ2π
3. Setting Up the Conditions:
- We need to compare the maximum particle speed and wave speed under different conditions of A0 and λ.
- We will analyze the conditions:
- λ2π>A0
- λ2π=A0
- λ2π<A0
4. Analyzing Each Condition:
- Condition 1: If λ2π>A0
- This implies vmax<v because:
ωA0ωλ2π<1⟹vmax<v
- Condition 2: If λ2π=A0
- This implies vmax=v because:
ωA0ωλ2π=1⟹vmax=v
- Condition 3: If λ2π<A0
- This implies vmax>v because:
ωA0ωλ2π>1⟹vmax>v
5. Conclusion:
- Based on the analysis:
- If λ2π>A0, then vmax<v.
- If λ2π=A0, then vmax=v.
- If λ2π<A0, then vmax>v.
- Therefore, the correct option is that when λ2π=A0, the maximum particle speed is equal to the wave speed.
- The wave speed (v) is given by the formula:
v=ωk
- The maximum particle speed (v_max) is given by:
vmax=ωA0
where ω is the angular frequency and A0 is the amplitude of the wave.
- The wave number k is defined as:
k=2πλ
- Therefore, substituting k into the wave speed formula gives:
v=ω2πλ=ωλ2π
- We need to compare the maximum particle speed and wave speed under different conditions of A0 and λ.
- We will analyze the conditions:
- λ2π>A0
- λ2π=A0
- λ2π<A0
- Condition 1: If λ2π>A0
- This implies vmax<v because:
ωA0ωλ2π<1⟹vmax<v
- Condition 2: If λ2π=A0
- This implies vmax=v because:
ωA0ωλ2π=1⟹vmax=v
- Condition 3: If λ2π<A0
- This implies vmax>v because:
ωA0ωλ2π>1⟹vmax>v
- Based on the analysis:
- If λ2π>A0, then vmax<v.
- If λ2π=A0, then vmax=v.
- If λ2π<A0, then vmax>v.
- Therefore, the correct option is that when λ2π=A0, the maximum particle speed is equal to the wave speed.
Topper's Solved these Questions
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSIGNMENT SECTION-II SUBJECTIVE
Explore 27 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSIGNMENT SECTION-II MCQ (SINGLE CORRECT)
Explore 47 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:NUMERICAL BASED QUESTIONS
Explore 2 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
Similar Questions
Knowledge Check
Both strings shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is v1and∈CDitisv2. Then v1v2 is
 A1B2C√2D1√2
A1B2C√2D1√2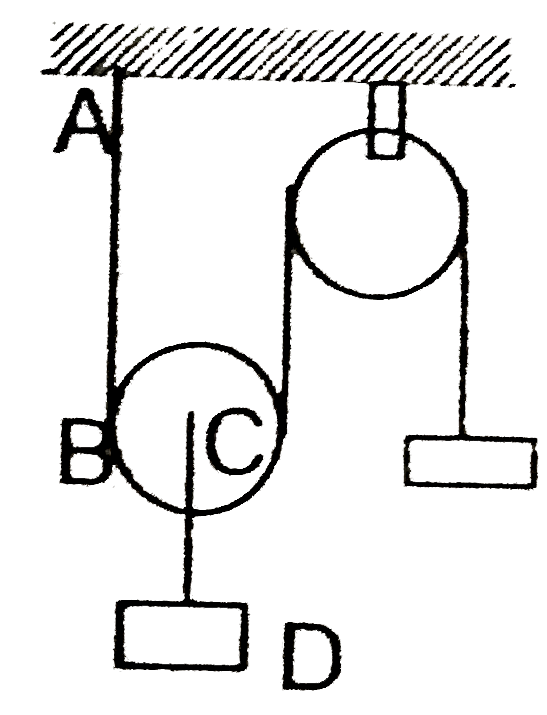
Both the strings shown in figure are mode of same material and have same cross-section. The pulleys are light the wave speed of a transverse wave in the string AB is v1 and in CD it is v2. Then v1/v2 isA1B2C√2D1/√2The velocity of a transverse wave in a string depends upon
Alength of the stringBtension applied onlyCtemperatureDtension in the string and the linear density of the material
The length, mass and tension of a string are 1000 cm, 0.01 Kg and 10 N respectively. The speed of transverse waves in the string will be -
View SolutionA string is stretched by a force of 40 newton. The mass of 10 m length of this string is 0.01 kg. the speed of transverse waves in this string will be
View SolutionA string 1m long is drawn by a 300 Hz vibrator attached to its end. The string vibrates in three segments. The speed of transverse waves in the string is equal to
View SolutionThe amplitude of a transverse wave on a string is 4.5 cm. The ratio of the maximum particle speed to the speed of the wave is 3:1. What is the wavelengtlı (in cm) of the wave?
View SolutionBoth the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of transverse wave in the string AB is v1 and in CD it is v2, the v1/v2 is

View Solution