An alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
E0ωLsin(ωt+π/2)
E0ωLsin(ωt−π/2)
E0ωLsin(ωt−π/2)
E0ωLsin(ωt+π/2)
The correct Answer is:B
To solve the problem of finding the current flowing through a coil of inductor L when an alternating voltage E=E0sin(ωt) is applied, we can follow these steps:
1. Understand the relationship between voltage and current in an inductor:
The voltage across an inductor is given by the formula:
VL=LdIdt
where VL is the voltage across the inductor, L is the inductance, and dIdt is the rate of change of current with respect to time.
2. Substitute the given voltage into the equation:
We know that the applied voltage is:
E=E0sin(ωt)
Therefore, we can set up the equation:
E0sin(ωt)=LdIdt
3. Rearrange the equation to isolate dI:
Rearranging the equation gives:
dIdt=E0sin(ωt)L
Now, we can separate the variables for integration:
dI=E0Lsin(ωt)dt
4. Integrate both sides:
We will integrate both sides. The left side integrates to I, and the right side requires integrating sin(ωt):
I=∫E0Lsin(ωt)dt
The integral of sin(ωt) is:
−1ωcos(ωt)
Therefore, we have:
I=−E0Lωcos(ωt)+C
where C is the constant of integration.
5. Express the current in terms of sine function:
We can express the cosine function in terms of sine:
cos(ωt)=sin(ωt+π2)
Thus, we can rewrite the current as:
I=E0Lωsin(ωt−π2)+C
6. Determine the constant of integration:
If we assume that at t=0, the current I is zero (initial condition), we can find C:
0=E0Lωsin(0−π2)+C
Since sin(−π2)=−1:
0=−E0Lω+C⟹C=E0Lω
7. Final expression for current:
Substituting C back into the equation for I:
I=E0Lωsin(ωt−π2)+E0Lω
Final Result:
The current flowing through the circuit at any instant is:
I(t)=E0Lωsin(ωt−π2)
The voltage across an inductor is given by the formula:
VL=LdIdt
where VL is the voltage across the inductor, L is the inductance, and dIdt is the rate of change of current with respect to time.
We know that the applied voltage is:
E=E0sin(ωt)
Therefore, we can set up the equation:
E0sin(ωt)=LdIdt
Rearranging the equation gives:
dIdt=E0sin(ωt)L
Now, we can separate the variables for integration:
dI=E0Lsin(ωt)dt
We will integrate both sides. The left side integrates to I, and the right side requires integrating sin(ωt):
I=∫E0Lsin(ωt)dt
The integral of sin(ωt) is:
−1ωcos(ωt)
Therefore, we have:
I=−E0Lωcos(ωt)+C
where C is the constant of integration.
We can express the cosine function in terms of sine:
cos(ωt)=sin(ωt+π2)
Thus, we can rewrite the current as:
I=E0Lωsin(ωt−π2)+C
If we assume that at t=0, the current I is zero (initial condition), we can find C:
0=E0Lωsin(0−π2)+C
Since sin(−π2)=−1:
0=−E0Lω+C⟹C=E0Lω
Substituting C back into the equation for I:
I=E0Lωsin(ωt−π2)+E0Lω
The current flowing through the circuit at any instant is:
I(t)=E0Lωsin(ωt−π2)
Topper's Solved these Questions
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSIGNMENT SECTION-II SUBJECTIVE
Explore 27 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:ASSIGNMENT SECTION-II MCQ (SINGLE CORRECT)
Explore 47 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:NUMERICAL BASED QUESTIONS
Explore 2 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Numerical Based Question Decimal Type
Explore 6 Videos
Similar Questions
An voltage, E=E0sinωt is applied acorss an inductor L. Obtain an expression for the current.
View SolutionExplain the term 'inductive reactance'.Show graphically the variation of inductive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied across a pure inductor L.Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.
View Solution
Knowledge Check
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)The alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
AI=I0sinωtBI=I0sin(ωt+π2)CI=I0sin(ωt−π2)DI=I0sin(ωt−π)
An a.c. voltage V=Vm sin ot is applied across an inductor L. Obtain an expression for current I.
View SolutionExplain the term 'capacitive reactance'.Show graphically the variation of capacitive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied a across a pure capacitor C.Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2
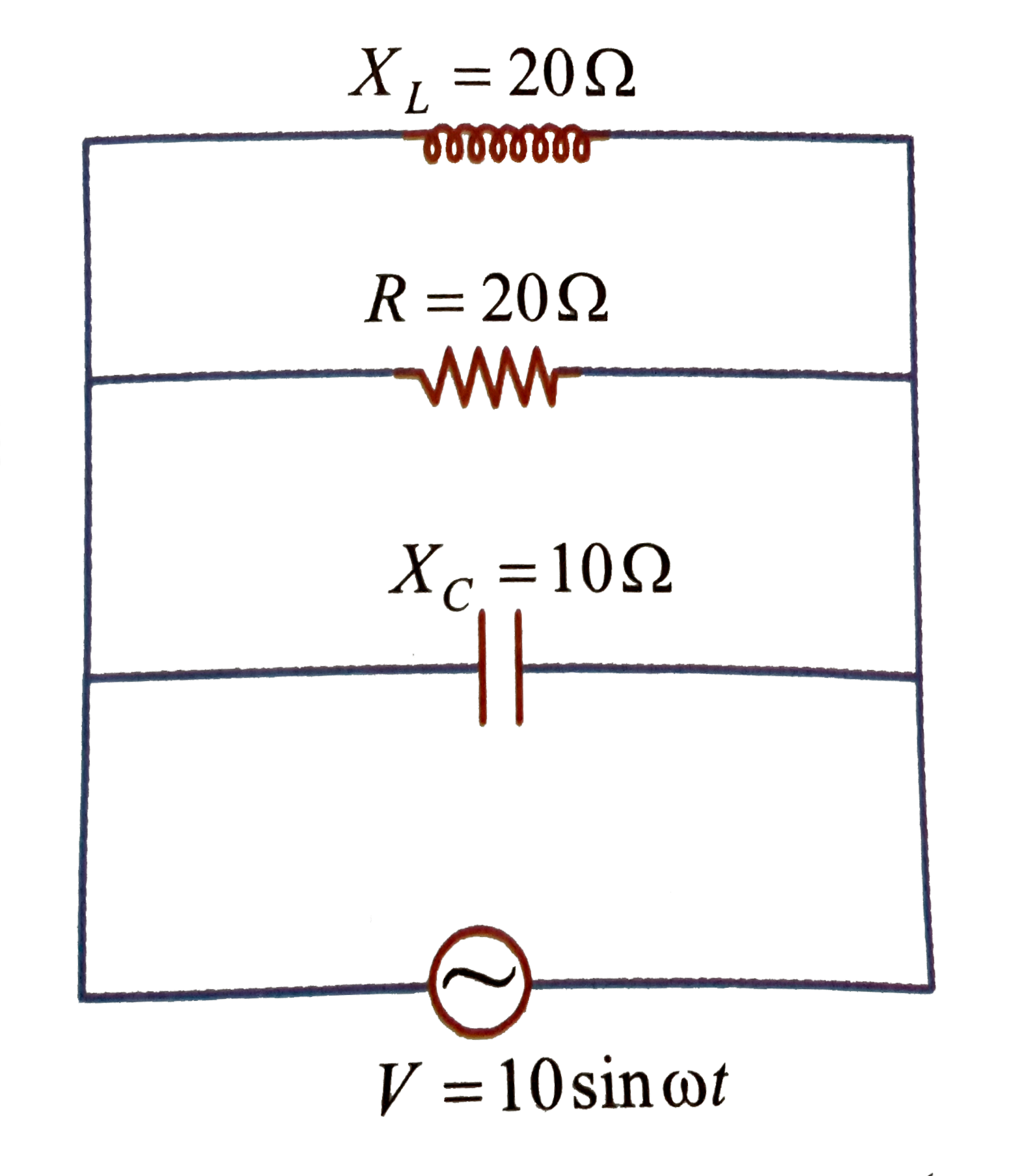
View SolutionAn alternative voltage V=10sinωt (in volts) is applied across a parallel arrangement as shown current (in A) through the source is best described by
View SolutionAn alternating emf, e=300 sin100πt volt, is applied to a pure resistance of 100 Ω. The rms current through the circuit is
View SolutionWhen an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
View Solution

