The potential of the field inside a charged sphere depends upon the distance from its centre to the point under consideration in the following way:
V=arn+b, where a and b are constants
If the charge is uniformly distributed within the sphere, then the value of n is
2
−2
1
−1
The correct Answer is:A
To solve the problem, we need to find the value of n in the potential equation V=arn+b for a uniformly charged sphere.
1. Understanding the Potential Inside a Charged Sphere:
For a uniformly charged sphere, the potential V at a distance r from the center (where r is less than the radius R of the sphere) is given by the formula:
V=KQ2R(3−r2R2)
where K is the Coulomb's constant, Q is the total charge of the sphere, and R is the radius of the sphere.
2. Rearranging the Formula:
We can rewrite the potential equation:
V=KQ2R⋅3−KQ2R3r2
This can be expressed as:
V=(−KQ2R3)r2+3KQ2R
3. Identifying Constants:
From the equation V=arn+b, we can identify:
- a=−KQ2R3
- b=3KQ2R
4. Comparing Powers of r:
In the equation V=arn+b, the term involving r is arn. From our rearranged potential equation, we see that the term involving r is −KQ2R3r2.
5. Finding the Value of n:
Since the term r2 corresponds to rn, we can conclude that:
n=2
Final Answer:
The value of n is 2.
---
For a uniformly charged sphere, the potential V at a distance r from the center (where r is less than the radius R of the sphere) is given by the formula:
V=KQ2R(3−r2R2)
where K is the Coulomb's constant, Q is the total charge of the sphere, and R is the radius of the sphere.
We can rewrite the potential equation:
V=KQ2R⋅3−KQ2R3r2
This can be expressed as:
V=(−KQ2R3)r2+3KQ2R
From the equation V=arn+b, we can identify:
- a=−KQ2R3
- b=3KQ2R
In the equation V=arn+b, the term involving r is arn. From our rearranged potential equation, we see that the term involving r is −KQ2R3r2.
Since the term r2 corresponds to rn, we can conclude that:
n=2
The value of n is 2.
Topper's Solved these Questions
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:MCQ
Explore 21 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Assertion-Reasoning MCQ
Explore 12 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Section (I) : Subjective
Explore 4 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:COMPREHENSION - IV
Explore 2 Videos
Similar Questions
The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b, where r is distance from the center of the ball, a and b are constants. Calculate the charge density inside the ball.
View SolutionFind the electric field at an arbitrary point of a sphere carrying a charge uniformly distributed over its volume.
View Solution
Knowledge Check
The potential inside a charged ball depends only on the distance r of the point form its centre according to the following relation V=Ar2+Bvo<s The charge density inside the ball will be
A−6ε0B6ε0C−3ε0ArD−6ε0ArThe electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A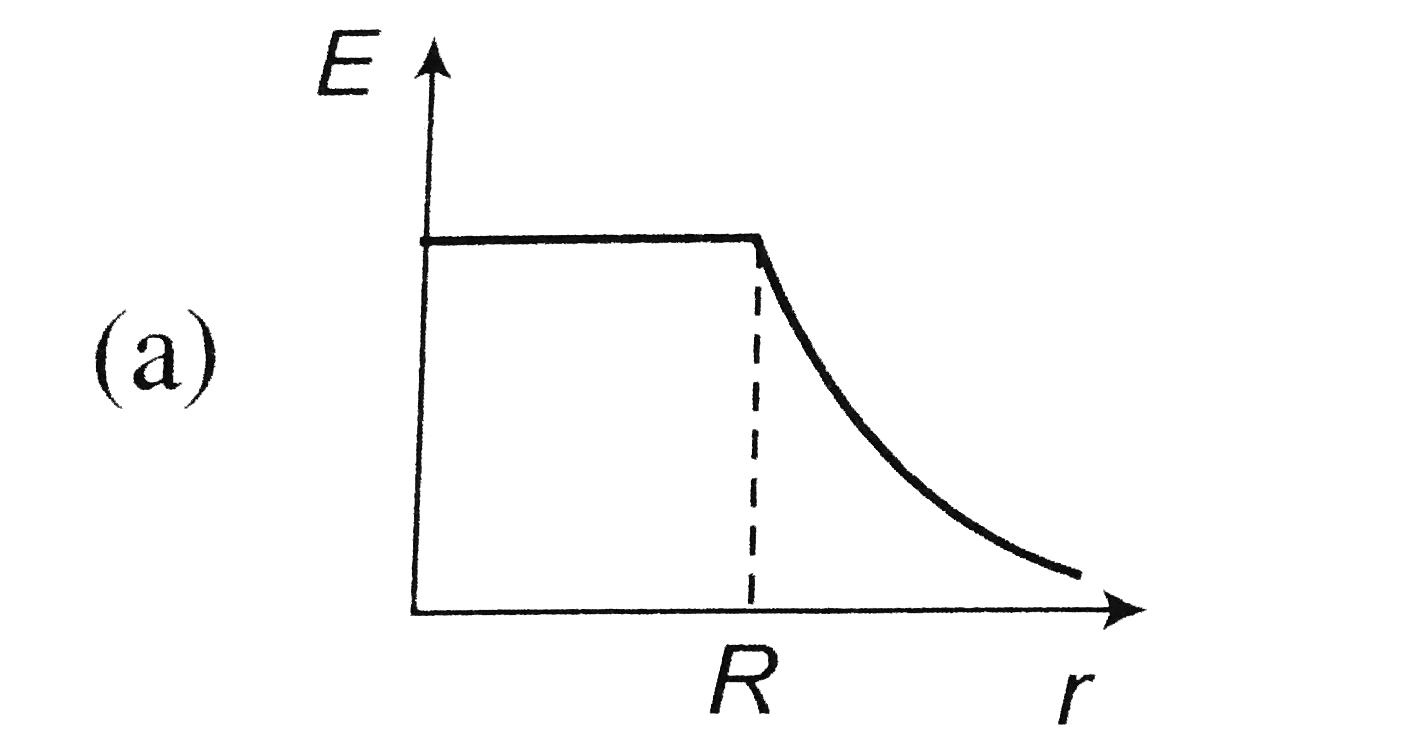 B
B C
C D
D
→E due to uniformly charged sphere of radius R as a function of distance from its centre is represented by
A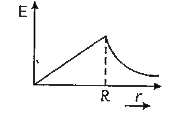 B
B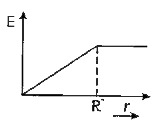 C
C D
D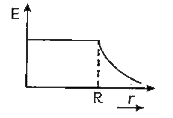
The centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
View Solution→E due to uniformly charged sphere of radius R as a function of distance from its centre is represented by:
View SolutionGraphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
View SolutionThe electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View Solution

