कोई लड़ाकू जहाज 1.5 km की ऊंचाई पर 720 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है। ऊर्ध्वाधर से तोप की नाल का क्या कोण हो जिससे 600ms−1 की चाल से दागा गया गोला वायुयान पर वार कर सके। वायुयान के चालक को किस न्यूनतम ऊंचाई पर जहाज को उड़ाना चाहिए जिससे गोला लगने से बच सके।
दिया गया हैलड़ाकू विमान का वेग vp = 720 किमी./घंटा
=720×10003600m/s
=200m/s
गोले की चाल u. = 600 मी./से.
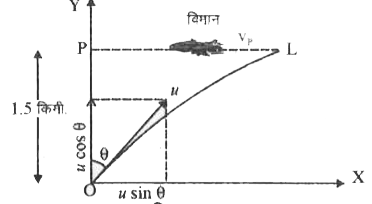
(i) माना तोप ऊर्ध्वाधर से θ कोण पर दागी गयी है।
अतः u का क्षैतिज घटक ux−usinθ
तथा u का ऊर्ध्वाधर घटक uy=ucosθ
माना कि गोला दागने के पश्चात् t समय में वायुयान को भेदता है |
t समय में वायुयान द्वारा तय दूरी
xP=vPt=200t ....(1)
t समय में गोले द्वारा तय क्षैतिज दूरी
xS=uxt
xS=(usinθ)t
⇒xS=(600sinθ)t ....(2)
गोला वायुयान को भेदेगा यदि
xP=xS
⇒200t=(600sinθ)t
⇒sinθ=200600=13
⇒θ=sin−1(13)
(ii) वायुयान के चालक को तोप के वार से बचने के लिए वायुयान को गोले की अधिकतम ऊँचाई के बराबर या अधिक रखना होगा।
∴ गोले द्वारा प्राप्त अधिकतम ऊँचाई
hm=u2y2g=(ucosθ)22g
=u2cos2θ2g
=(600)2(cos19.5∘)22×10
hm=600×600×8/92×10
[∵cos2=1−sin2θ=1−(13)2=89]
hm=1600m
=16m
अतः गोले के वार से बचने के लिए वायुयान को कम से कम 16 किमी. ऊँचाई पर उड़ाना होगा।
Related Playlists
- BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (लघुतयात्मक प्रश्न )8videos
समतल में गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (निबन्धात्मक प्रश्न)5videos
समतल में गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - NCERT TEXTBOOK PROBLEMS25videos
समतल में गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - मात्रक एवं मापन EXERCISE - आंकिक प्रश्न21videos
मात्रक एवं मापन
- BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न आंकिक प्रश्न (एक समान त्वरित गति पर आधारित प्रश्न)19videos
सरल रेखा में गति
Similar Questions
अदिश व सदिश राशियाँ क्या हैं? प्रत्येक के तीन-तीन उदाहरण दीजिये।
04:43View Solutionसदिश संयोजन का बहुभुज नियम लिखिये।
04:06View Solutionनिम्नलिखित भौतिक राशियों में से बतलाइए कि कौम-सी सदिश हैं और कौन-सी अदिश : आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।
View Solutionहवा में ध्वनि का वेग 332 m/s है यदि उसकी लम्बाई को किलोमीटर में तथा समय को घण्टे में नापा जाये तो वेग का नया मान क्या होगा ?
06:00View Solutionएक पिण्ड विरामावस्था से प्रारंभ कर 20मी./से.^2 त्वरण से गति करता है। 6वें सेकण्ड में तय की गई दूरी का मान ज्ञात करो।
04:00View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
03:40View Solutionएक वायु सेना का जहाज 100 किमी/घण्टा की दर से ऊर्ध्वाधरतः ऊपर की और चढ़ रहा है। यदि पृथ्वी की त्रिज्या r किमी है , तब इसके उड़ना शुरू के मिनट बाद जहाज से दिखाई देने वाले पृथ्वी का क्षेत्रफल A=2πr2hr+h जहाँ , h जहाज की पृथ्वी से दूरी है )
06:32View Solutionजॉर्ज पंचम की नाक' पाठ के माध्यम से लेखक ने समाज पर क्या व्यंग्य किया है?
03:47View Solution2 m ऊंचाई का आदमी 6 m ऊंचे बिजली के खंभे से दूर 5 km/h की समान चाल से चलता है| उसकी छाया की लमबायी की वृद्धि की दर ज्ञात कीजिए |
View SolutionIf a boat goes upstream at a speed fo 18 km /hr and comes back the same distance at 30 km/ hr.What is the average speed (in km /hr)for the total journey?
कोई नाव धारा के विपरीत दिशा में 10 किलोमीटर /घंटा की चाल से चलती है और समान दूरी पर 30 किलोमीटर/घंटा की चाल से वापस आती है। कुल यात्रा के लिए औसत चाल किलोमीटर/ घंटा में) क्या है?01:57View SolutionThe angle of elevation of an aeroplane from a point on the ground is 60∘. After flying for 30 seconds, the angle of elevation changes to 30∘. If the aeroplane is flying at a height of 4500 m,then what is the speed (in m/s) of aeroplane?
मैदान पर एक बिन्दु से एक हवाई जहाज का उन्नयन कोण 60∘ है। 30 सेकण्ड उड़ने के पश्चात कोण 30∘ में परिवर्तित हो जाता हे। यदि हवाई जहाज 4500 मी. की ऊँचाई पर उड़ रहा है, तो हवाई जहाज की गति (मी./से. में) क्या है?05:29View SolutionAn aeroplane flying horizontally at a height of 3 Km. above the ground is observed at a certain point on earth to subtend an angle of 60^@ . After 15 sec flight, its angle of elevation is changed to 30^@ . The speed of the aeroplane (taking sqrt3 = 1.732) is- कोई वायुयान पृथ्वी की सतह से 3 कि.मी. ऊपर क्षेतिज उड़ रहा है। पृथ्वी से किसी बिन्दु से यह देखने में आता है कि वह 60^@ के कोण पर कक्षांतरित होता है। 15 सेकण्ड बाद उसका उन्नयन कोण 30^@ परिवर्तित हो जाता हैं वायुयान की चाल बताइए। ( sqrt3 =1.732)
02:41View SolutionA telegraph post is bent at a point above the ground due to storm. Its top just touches the ground at a distance of 10 sqrt3 m from its foot and makes an angle of 30^@ with the horizontal. Then length (in metres) of the telegraph post is एक टेलीग्राफ का खंभा आँधी के कारण भूमि के ऊपर एक बिन्दू पर झुक गया है। उसका शीर्ष उसके पाद से 10 sqrt3 की दूरी पर ,भूमि को स्पर्श कर रहा है और क्षैतिज रूप से 30^@ का एक कोण बना रहा है। टेलीग्राफ के खंभे की लम्बाई (मीटर में) कितनी है?
02:14View Solution'दरबार' कविता के माध्यम से किस पर अपनी तीखी प्रतिक्रिया । व्यक्त की है?
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक जहाज 'A' 10 किमी/घं की चाल से पश्चिम दिशा की ओर गति कर रहा है। एक अन्य जहाज 'B इस जहाज A से 100 किमी दक्षिण दिशा में है और 10 किमी/घं की चाल से उत्तर दिशा की ओर जा रहा है। इन दोनों के बीच की दूरी कितने समय के पश्चात् न्यूनतम हो जायेगी?
View Solution


