How time period of a simple pendulum depends on the acceleration due to gravity ?
To determine how the time period of a simple pendulum depends on the acceleration due to gravity, we can follow these steps:
Step 1: Understand the formula for the time period of a simple pendulum
The time period (T) of a simple pendulum is given by the formula:
T=2π√Lg
where:
- T is the time period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
Step 2: Analyze the relationship between T and g
From the formula, we can see that:
- The time period T is directly related to the square root of the length L and inversely related to the square root of the acceleration due to gravity g.
- This means that if L is constant, then T is inversely proportional to √g.
Step 3: Determine the effect of changing g on T
- If the value of g increases (for example, if the pendulum is moved to a location with stronger gravity), the time period T will decrease because of the inverse relationship.
- Conversely, if the value of g decreases (for example, if the pendulum is taken to the Moon where gravity is weaker), the time period T will increase.
Step 4: Consider the effective gravity in different situations
- The effective gravity can change in different scenarios, such as when the pendulum is in an accelerating lift. For instance:
- If the lift accelerates upwards, the effective gravity geffective increases, leading to a shorter time period.
- If the lift accelerates downwards, the effective gravity geffective decreases, leading to a longer time period.
Conclusion
In summary, the time period of a simple pendulum is inversely proportional to the square root of the acceleration due to gravity. As gravity increases, the time period decreases, and as gravity decreases, the time period increases.
---
The time period (T) of a simple pendulum is given by the formula:
T=2π√Lg
where:
- T is the time period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
From the formula, we can see that:
- The time period T is directly related to the square root of the length L and inversely related to the square root of the acceleration due to gravity g.
- This means that if L is constant, then T is inversely proportional to √g.
- If the value of g increases (for example, if the pendulum is moved to a location with stronger gravity), the time period T will decrease because of the inverse relationship.
- Conversely, if the value of g decreases (for example, if the pendulum is taken to the Moon where gravity is weaker), the time period T will increase.
- The effective gravity can change in different scenarios, such as when the pendulum is in an accelerating lift. For instance:
- If the lift accelerates upwards, the effective gravity geffective increases, leading to a shorter time period.
- If the lift accelerates downwards, the effective gravity geffective decreases, leading to a longer time period.
Conclusion
In summary, the time period of a simple pendulum is inversely proportional to the square root of the acceleration due to gravity. As gravity increases, the time period decreases, and as gravity decreases, the time period increases.
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Revision Exercises (Additional Question )
Explore 3 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Revision Exercises (fill in the blanks)
Explore 9 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:HOTS (Higher Order Thinking Skills & Advanced Level)
Explore 11 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
Knowledge Check
Time period of simple pendulum is
AT=2π√lgBT=2π√glCT=√2πlgDT=12π√glConsider a simple pendulum. The period of oscillation of the simple pendulum depends on its length and acceleration due to gravity. Then the expression for its time period is
At=kg√lBt=k√lgCt=k√lgDt=kl√g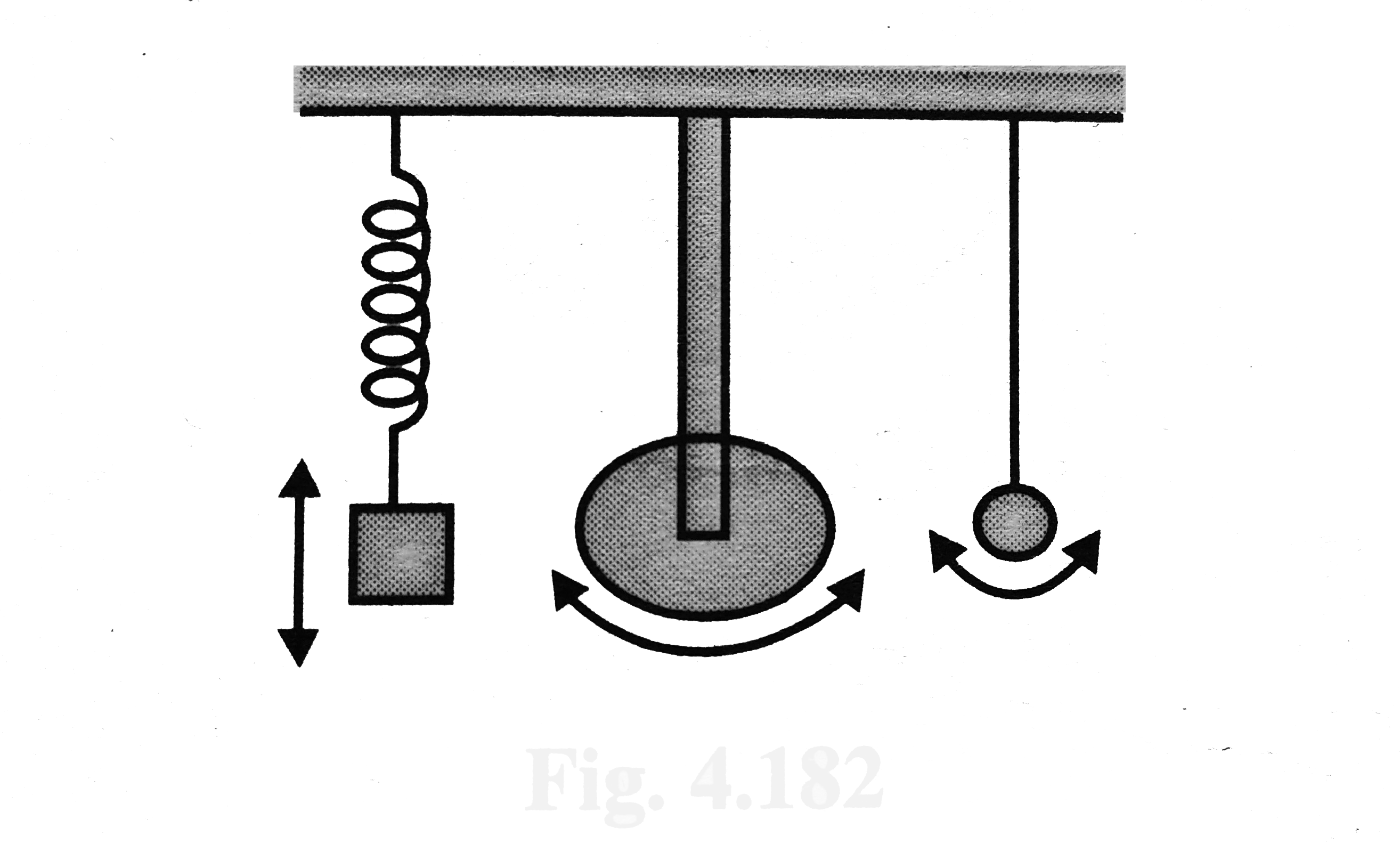
Q. Statement I Three pendulums are suspended from ceiling as shown in Fig. These three pendulums are set to oscillate as shon by arrows, and it is found that all three have same time period. Noe, all three are taken to a place where acceleration due to gravity changes to 4/9th of its value at the first place. If spring pendulum makes 60 cycles in a given time at this place, then torsion pendulum and simple pendulum will also make 60 oscillation in same (given) time interval. Statement II: Time period of torsion pendulum is independent of acceleration due to gravity.AStatement I is true statement II is true, Statement II is a correct explanation for Statement I.BStatement I is true statement II is true, Statement II is NOT a correct explanation for Statement I.CStatement I is true, Statement II is falseDStatement I is false, Statement II is true
Calculate the tiem period of a simple pendulum of length one meter. The acceleration due ot gravity at the place is π2ms−2.
View SolutionThe time period of a simple pendulum depends on its _______.
View SolutionTime period of simple pendulum increase with
View SolutionIf the time period of a two meter long simple pendulum is 2s, the acceleration due to gravity at the place where pendulum is executing S.H.M. is:
View SolutionThe period of oscillation of a simple pendulum at a given place with acceleration due to gravity 'g' depends on
View Solution

