Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

When the mass is displaced from equilibrium position by adistance x, the total restoring force due to both the springs will be towards left and is given by
F=F1+F2=−kx+(−hx)=−2kx.
Negative sign means that the direction of force F is opposite to direction of x.
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:NCERT Exemplar Problems Subjective Question ( short Answer Type Questions )
Explore 6 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:HOTS (Higher Order Thinking Skills & Advanced Level)
Explore 11 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:NCERT Exemplar Problems Subjective Question (Multiple Choice Questions (Type-II))
Explore 7 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
Tow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
Two springs of spring constant 6N/m and 4N/m are attached to a block of mass 1 kg and to fixed support. Then time period of the given oscillation is
(consider √10=π)A1sB2sC0.5sD4sA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kTwo springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :
 AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
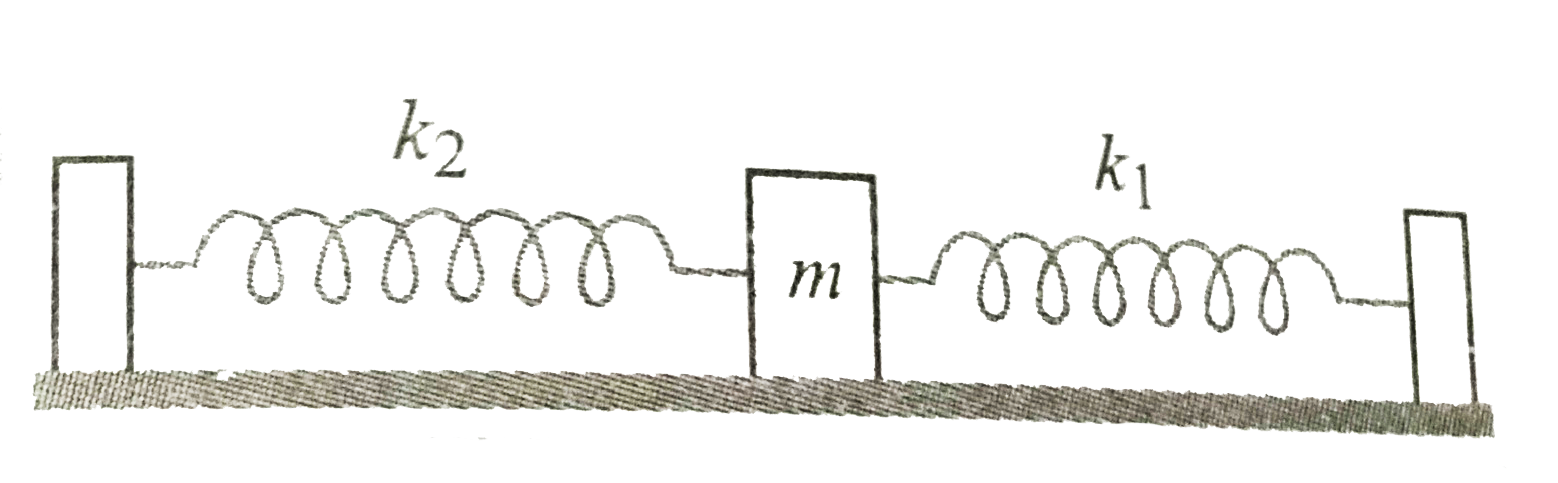
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
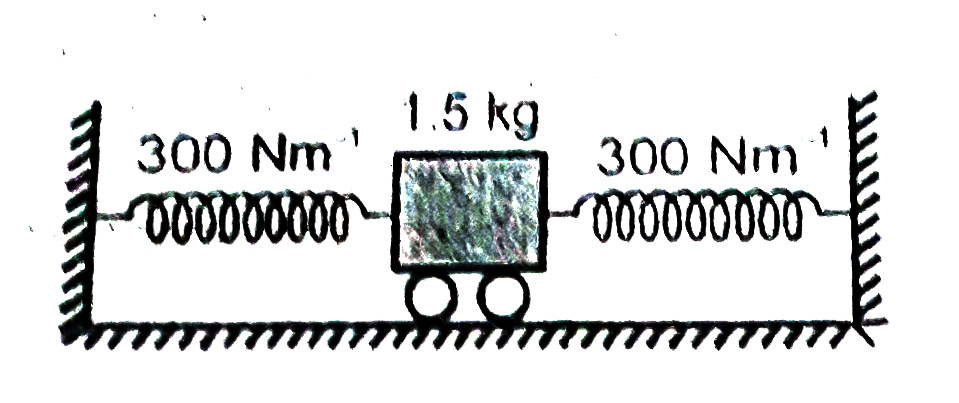
View Solution

