In the figure AD is the external bisector of $∠ E A C$ , intersects BC produced to D. IF $A B = 12 c m, A C = 8 c m and B C = 4 c m$ , find CD :

A

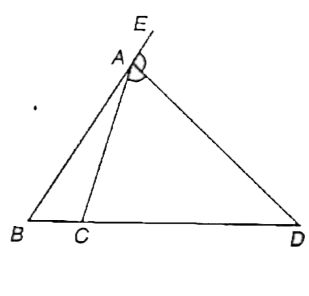
10 cm

B

6 cm

C

8 cm

D

9 cm

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

|

Answer

Step by step video, text & image solution for In the figure AD is the external bisector of angleEAC, intersects BC produced to D. IF AB = 12 cm, AC = 8cm and BC = 4 cm, find CD : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The internal /external bisector of an angled of a triangle divides the opposite side internally / externally in the ratio of the sides containing the angle .
In the given figure ,Ae is the bisector of the exterior $∠ C A D$ meeting BC produced in E . If AB=15 cm , AC = 8 cm and BC =14 cm , find CE .

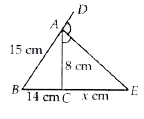A12 cm
B16 cm
C20 cm
D18 cm
Question 2 - Select One
In $△ A B C$ , AD is the internal bisector of $∠ S$ , meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then $A B : A C$ is:
A $3 : 5$
B $4 : 5$
C $1 : 2$
D $2 : 1$
Question 3 - Select One
In the given figure , Ad is the bisector of $∠ B A C$ . If AB = 10 cm , AC = 14 cm and BC = 8 cm , find BD and DC respectively .

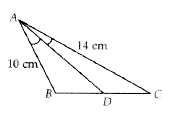A $4.7 c m, 3.3 c m$
B $3.3 c m, 4.7 c m$
C $4.3 c m, 3, 5 c m$
D $3.5 c m, 4.3 c m$

ARIHANT SSC-GEOMETRY-INTRODUCTORY EXERCISE - 12.2

Home
Ask Doubt
Profile