State and prove prism formula.
Video Solution
Text Solution
Refraction. The phenomenon of change in path of a ray of light as it passes from one medium into another is called refraction.
Let a ray DE strikes the face AB of the prism at an angle of incidence i and emerges out at an angle e. Let r1 and r2 be the angles of refraction and δ be exterior angle of deviation.
δ is exterior angle of triangle HEF
∴δ=1+2=(i−r1)+(e−r2)
or δ=i+e−(r1+r2) ...(1)
In quadrilateral AEOF, we have
∠AEO+A+∠AFO+∠O=360∘
or 90∘+A+90∘+∠O=360∘
or A+∠O=180∘
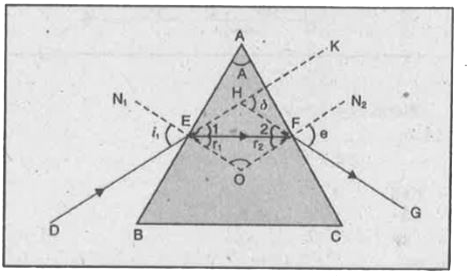
Also, in triangle FEO,
r1+r2+∠O=180∘
A+∠O=r1+r2+∠O
or A=r1+r2 ...(ii)
Substituting in equation (i), we have
δ=i+e−A
or A+δ=i+e
For small angled prism,
At face AB,
sinisinr1=ir1=(μ)
or i=μr1
Similarly, at face AC,
e=μr2
Putting the value of i and e in equation (iii), we get
δ=μr1+μr2−A=μ(r1+r2)−A
Using equation (ii), we get
δ=(μ−1)A ...(iv)
If we repeat the experiment with different angles of incidence, then we get a graph as shown in the figure when i is increased, δ decreases first, reaches a minimum and starts increasing again. For a particular value of δ, there are two angles of incidence i1 and i2, At minimum deviation,
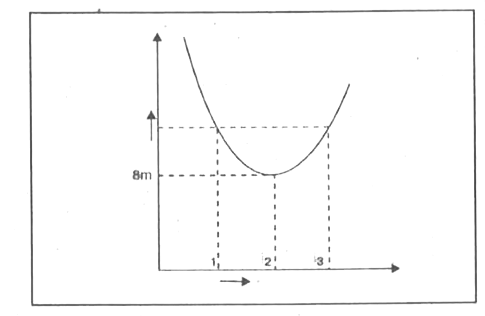
δ=δm and i1=i2=i
Hence r1=r2=r
∴r+r=2A or r=A2
And δm=i+i−A
or 2i=A+δm
or i=A+δm2
Now μ=sinisinr=sin(A+δm)2sin(A)2
|
Topper's Solved these Questions
- OPTICSBOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - OBJECTIVE TYPE QUESTIONS
26 Videos
- OPTICSBOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - SHORT ANSWER TYPE QUESTIONS
46 Videos
- MODEL TEST PAPER - 2BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER - 2EXERCISE - SET - D ( LONG ANSWER TYPE QUESTIONS)
4 Videos
- PRINCIPLES OF COMMUNICATIONBOOK - MBD -HARYANA BOARDCHAPTER - PRINCIPLES OF COMMUNICATIONEXERCISE - Objective Type Questions
19 Videos
Similar Questions
Define refractive index of a transparent medium. A ray of light passes through a triangular prism. Plot a graph showing the variation of angle of deviation with the angle of incidence. Hence derive prism formula.
View SolutionState and prove Baye's theorem.
View SolutionState and prove Gauss's law in electrostatics.
View SolutionState and prove theorem of perpendicular axes.
View SolutionState and prove theorem of parallel axes.
View SolutionState and explain Brewster's law of polarization.
View SolutionLaw of conservation of angular momentum
View SolutionState and prove the commutative property of vector addition.
View SolutionState and prove Hooke's law.
View SolutionState and prove the Pythagoras theorem.
View Solution
