A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .

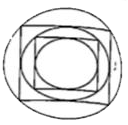
What is the radius of the inner - most circle ?

$\frac{R}{2}$

$\frac{R}{\sqrt{2}}$

$\sqrt{2 R}$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R . What is the radius of the inner - most circle ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS MENSURATION

Topper's Solved these Questions

Knowledge Check

A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .

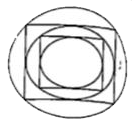
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?
A $(2 + \sqrt{3}) π R$
B $(3 + \sqrt{2}) π R$
C $3 \sqrt{3} π R$
Dnone of these
A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .

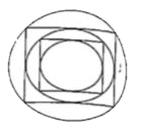
What is the sum of areas of all the squares shown in the figure ?
A $3 R^{2}$
B $3 \sqrt{2} R^{2}$
C $\frac{3}{\sqrt{2}} R^{2}$
Dnone of these
A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles is
A $4 π R^{2} (1 - {(\frac{1}{2})}^{n})$
B $2 π R^{2} (1 - {(\frac{1}{2})}^{n})$
C $3 π R^{2} (1 - {(\frac{1}{3})}^{n})$
D $π R^{2} (1 - {(\frac{1}{2})}^{n})$

ARIHANT SSC-MENSURATION-EXERCISE (LEVEL 2)

Home
Ask Doubt
Profile

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times. Sum of the areas of all circles is

ARIHANT SSC-MENSURATION-EXERCISE (LEVEL 2)

A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles is