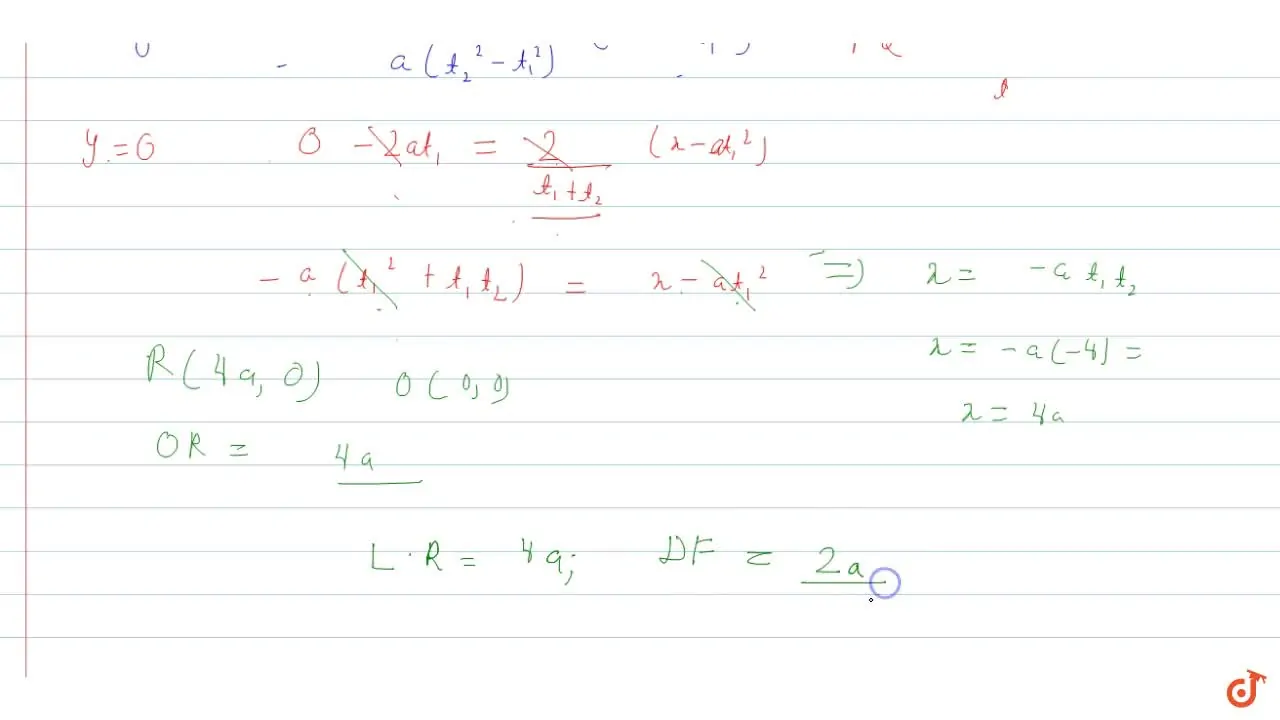Through the vertex 'O′ of the parabola y2=4ax, variable chords OPandOQ are drawn at right angles. If the variable chord PQ intersects the axis of x at R , then distance OR: (a)equals double the perpendicular distance of focus from the directrix. (b)equal the semi latus rectum of the parabola (c)equals latus rectum of the parabola (d)equals double the latus rectum of the parabola
Step by step video & image solution for Through the vertex ' O^(prime) of the parabola y^2=4a x , variable chords O Pa n dO Q are drawn at right angles. If the variable chord P Q intersects the axis of x at R , then distance O R : (a)equals double the perpendicular distance of focus from the directrix. (b)equal the semi latus rectum of the parabola (c)equals latus rectum of the parabola (d)equals double the latus rectum of the parabola by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
Through the vertex O of the parabola y2=4ax, variable chords OPandOQ are drawn at right angles. If the variables chord PQ intersects the axis of x at R, then distance OR
View SolutionFind the coordinates of the focus, axis, the equation of the directrix and latus rectum of the parabola y2=8x.
View SolutionProve that the semi-latus rectum of the parabola y^(2) = 4ax is the harmonic mean between the segments of any focal chord of the parabola.
View SolutionFind vertex, focus, directrix and latus rectum of the parabola y2+4x+4y−3=0.
View SolutionProve that the semi-latus rectum of the parabola y2=4ax is the harmonic mean between the segments of any focal chord of the parabola.
View SolutionFind the co-operate of the focus, the equation of the directrix and latus rectum of the parabola y2=20x.
View SolutionFind the vertex, focus, directrix, axis and latus-rectum of the parabola y2=4x+4y.
View SolutionFind the equations of the normals at the ends of the latus- rectum of the parabola y2=4ax. Also prove that they are at right angles on the axis of the parabola.
View SolutionFind the vertex, focus, directrix and length of the latus rectum of the parabola y2−4y−2x−8=0
View SolutionFind the coordinates of the focus and the vertex, the equations of the directix and the axis, and the lendth of the latus rectum of the parabola y2=8x
View Solution