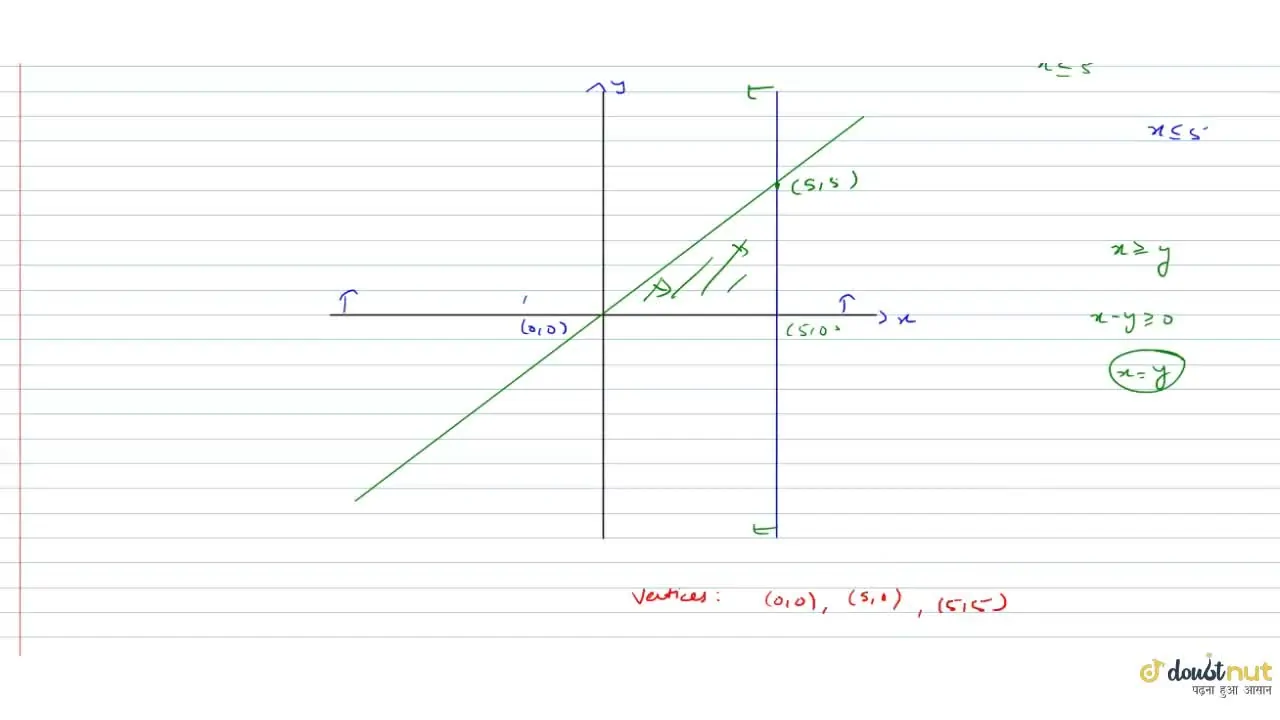
The solution of the system of inequalities is a polygonal region with the vertices as
(0,0),(5,0),(5,5)
(0,0),(0,5),(5,5)
(5,5), (0,5), (5,0)
(0,0), (0,5), (5,0)
The correct Answer is:A
Check the point which belongs the given inequations.
Related Playlists
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Level 215videos
LINEAR PROGRAMMING
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Level 310videos
LINEAR PROGRAMMING
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Easy type Question5videos
LINEAR PROGRAMMING
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-315videos
LIMITS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 315videos
LOGARITHMS
Similar Questions
The solution of the system of inequalities x≥0,y≥0,5x+2y≥10,6x+5y≤30 is a polygonal region with the vertices _________
View SolutionThe solution of the inequations x≥0,y≥0,y=2andx=2 form the polygonal region with the vertices (0,0),(0,2),(2,0) and (2,2) and the polygon so formed by joining the vertices is a _____
View SolutionThe graphical solution of the system of linear inequalities 3x,4y≥12,y≥1,x≥0 is
View SolutionSolution set of inequation x≥0 is
View SolutionThe shaded region representing the solution set of the system of inequalities x−2y≤3,3x+4y≥12,x≥0,y≥1 in the following figure is
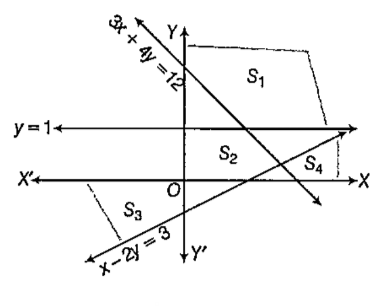 View Solution
View SolutionSolve the system of inequation:|x−1|≤5,|x|≥2.
View SolutionThe graphical solution of linear inequalities x+y≥5 and x−y≤3,
View SolutionThe graphical solution of the inequalities x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0 is
View SolutionThe region represented by the solution of system of inequalities 5x+4y≤40,x≥2,y≥3 is
View SolutionDraw the graph of the solution set of the system of inequations 2x+3y≤4,x≥0andy≥0.
View Solution