Minimize 3x+2y subject to the constraints $x + y \geq 5 and x + 2 y \geq 6, x \geq 0, y \geq 0$

Video Solution

Text Solution

Verified by Experts

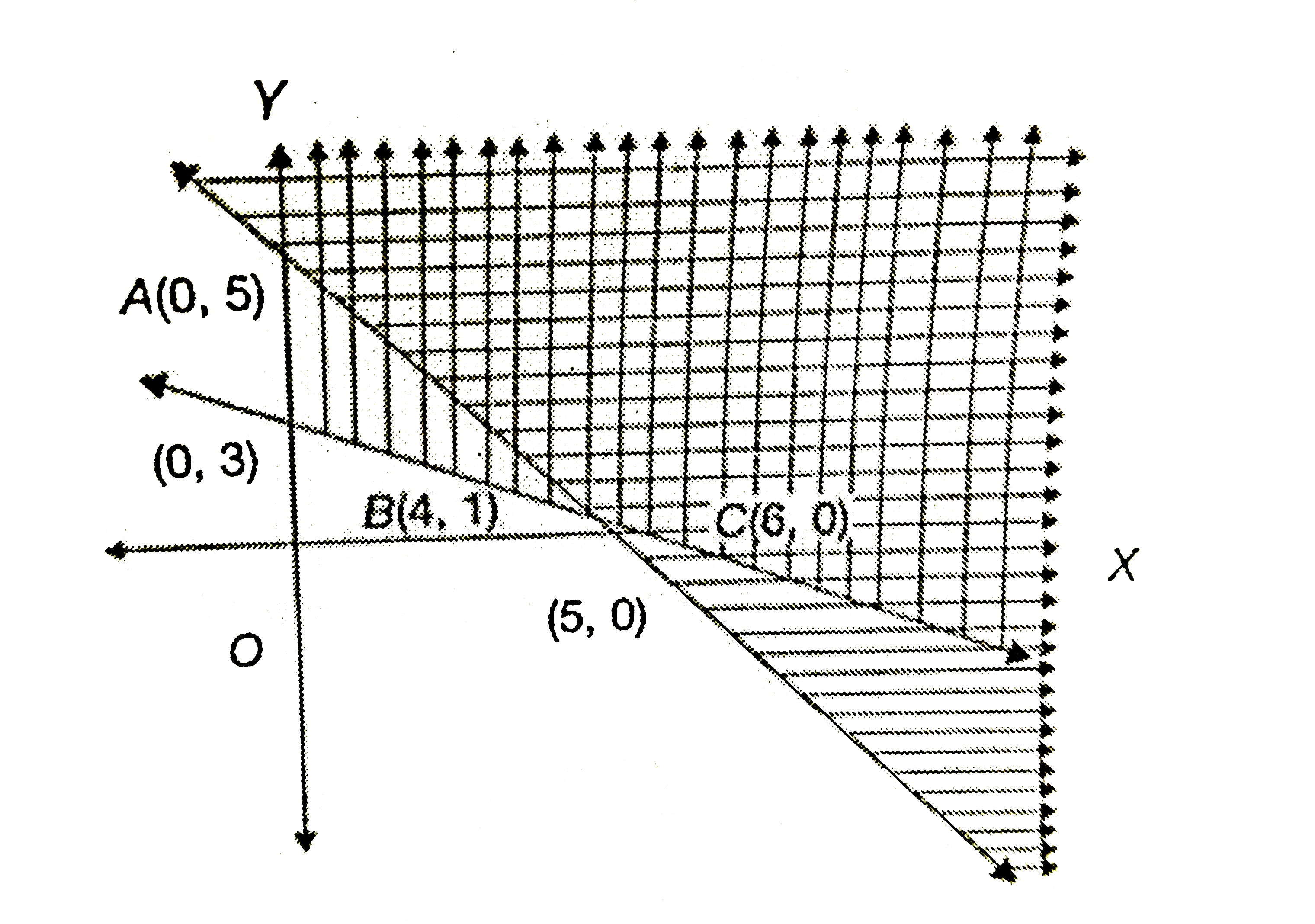
At $x \geq 0 and y \geq 0$ , the feasible region lies in the I quadrant .
The graph of $x + y \geq 5$ is shown with horizontal line, and the graph of $x + 2 y \geq 6$ is shown with vertical lines.
$∴$ The feasible region is that part of the I quadrant in which there are both horizontal and vertical lines.
At B(4,1),f(x,y)=3(4)+2(1)=14
At A(0,5), f(x,y)=3(0)+2(5)=10
At C(6,0), f(x,y)=3(6)+2(0)=18.
Clearly, f(x,y) is the minimum at A.

Updated on:21/07/2023

The linear programming problem minimiseZ=3x+2y subject to the constraints
$x + y \geq 8$
$3 x + 5 y \leq 15$
$x \geq 0, y \geq 0$ has
Aone solution
Bno feasible solution
Ctwo solutions
Dinfinitely many solution
Minimize Z= 3x+y, subject to constriants
$2 x + 3 y \leq 6, x + y \geq 1, x \geq 0, y \geq 0$ Then
Ax = 1, y = 1
Bx = 0, y = 1
Cx = 1, y = 0
Dx = - 1, y = - 1
The point at which the minimum value of $z = 8 x + 12 y$ subject to the constraints $2 x + y \geq 8, x + 2 y \geq 10 x \geq 0, y \geq 0$ is obtained is
A(8,0)
B(9, 1)
C(2, 4)
D(10, 0)