ABCD is square of side 4 cm. If E is point in the interior of the square such that ΔCED is equilateral, then find the area of ΔACE in cm2
A
2(√3−1)
B
4(√3−1)
C
6(√3−1)
D
8(√3−1)
Video Solution
Text Solution
The correct Answer is:B
(i) Draw the figure according to the data and draw ¯¯¯¯¯¯EF∣∣¯¯¯¯¯¯CD.
(ii) Area of △ACE= Area of the triangle ABC −{Area of △ECD+Area of ABED}.
|
Topper's Solved these Questions
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Level 2
20 Videos
- MATRICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICESEXERCISE - EXERCISE CONCEPT APPLICATION (LEVEL 3)
15 Videos
- MODULAR ARITHMETIC BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODULAR ARITHMETIC EXERCISE - Level 3
15 Videos
Similar Questions
Knowledge Check
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that △CED is equilateral, then find the area of △ACE (in cm2).
A2(√3−1)B4(√3−1)C6(√3−1)D8(√3−1)In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
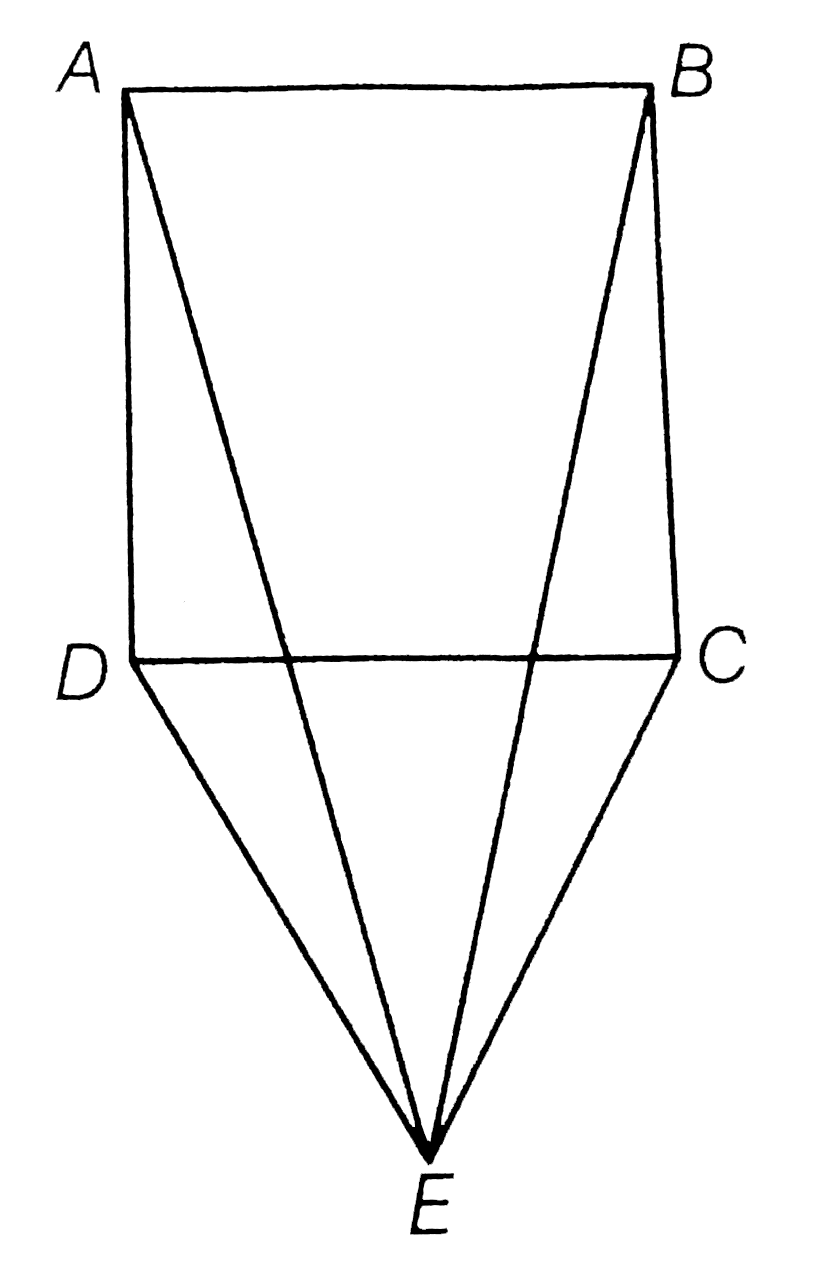 ARHSBSSSCAASDSAS
ARHSBSSSCAASDSASABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of these
if the side of equilateral triangle is 4cm find the area of ex circle
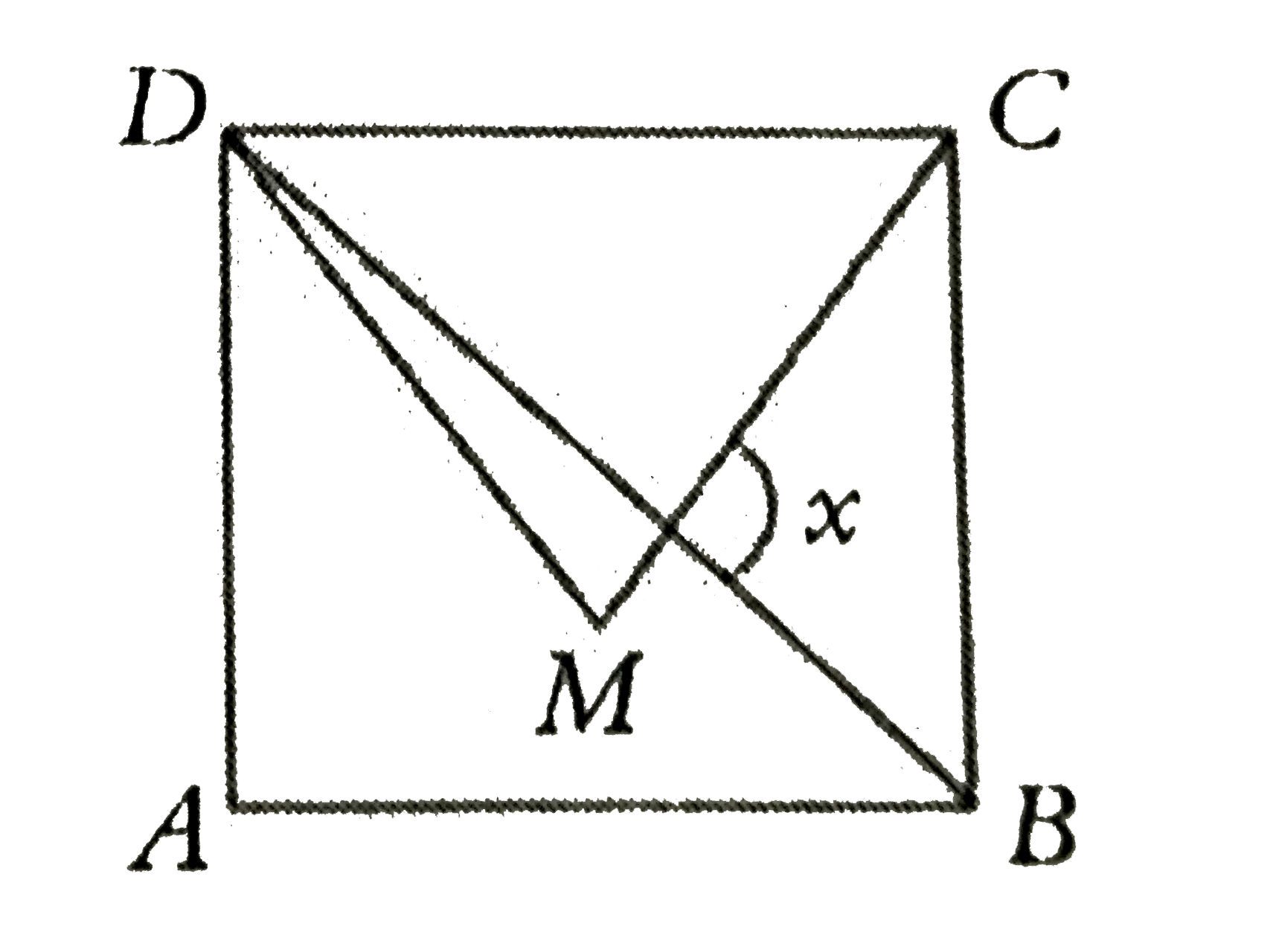
View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
View SolutionThe side of an equilateral triangle is 10 cm. Find its area (in cm2).
View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.

View SolutionThe ratio of the area of a square of side a and that of an equilateral triangle of side a, is
View Solution
